Введение

Взаимодействие электрических зарядов осуществляется посредством электрического поля. Каждый из зарядов создаёт электрическое поле, которое действует на все другие заряды, находящиеся в этом поле. Сила F, действующая на заряд q, помещённый в электрическое поле, определяется напряжённостью E поля в точке, где находится этот заряд (принцип близкодействия):

F = qE.

Наиболее наглядным представлением электрического поля является картина его силовых линий и эквипотенциальных поверхностей. Напомним, что силовой линией называется линия, касательная к которой в любой её точке имеет направление, совпадающее с направлением вектора напряжённости поля в той же точке. Эквипотенциальной поверхностью называется поверхность, во всех точках которой потенциал электрического поля имеет одно и то же значение. Через любую точку поля можно провести силовую линию и эквипотенциальную поверхность. Более подробно о свойствах силовых линий и эквипотенциальных поверхностей вы можете прочитать в приложениях к работе 1.

В настоящей работе вы сможете построить эти картины для любой системы зарядов, расположенных на плоскости (плоская система зарядов).

Выбор масштабов

Поскольку в работе картина линий поля строится на экране компьютера, то сразу же возникает вопрос о выборе масштабов этой картины. Поскольку мы ставим целью получить картину линий поля и изучить геометрические особенности этой картины, то масштабы могут быть выбраны достаточно произвольно. Действительно, картина силовых линий электрического поля не изменится, если все заряды, создающие поле, увеличить или уменьшить в одинаковое число раз. Тем самым, выбор абсолютных величин зарядов совершенно неважен, если только нас интересует именно геометрия силовых линий. Поэтому мы в дальнейшем будем указывать величины зарядов просто в виде чисел, никак не связывая эти числа с величиной заряда в тех или иных единицах (например, кулонах). Поэтому опускаем и множитель 1/4₀, поскольку конкретная величина напряжённости или потенциала для нас не будет играть никакой роли. Для нас интересным будет лишь направление вектора Е в данной точке поля и факт одинаковости потенциала  в различных точках эквипотенциальной поверхности.

Кроме того, картина линий поля не изменится и при одновременном изменении координат всех зарядов в одинаковое число раз. Это позволяет нам не интересоваться выбором масштабов расстояний, указывая их, так же как и заряды, в некоторых условных величинах.

Краткое описание алгоритма построения линий поля

Компьютер рассчитывает картину силовых линий и эквипотенциальных поверхностей на основе принципа суперпозиции. Для нахождения силовой линии необходимо найти направление вектора напряжённости электрического поля. Если заданы координаты зарядов и их величины, то напряженность поля в произвольной точке находится как сумма векторов напряженности поля каждого из зарядов:

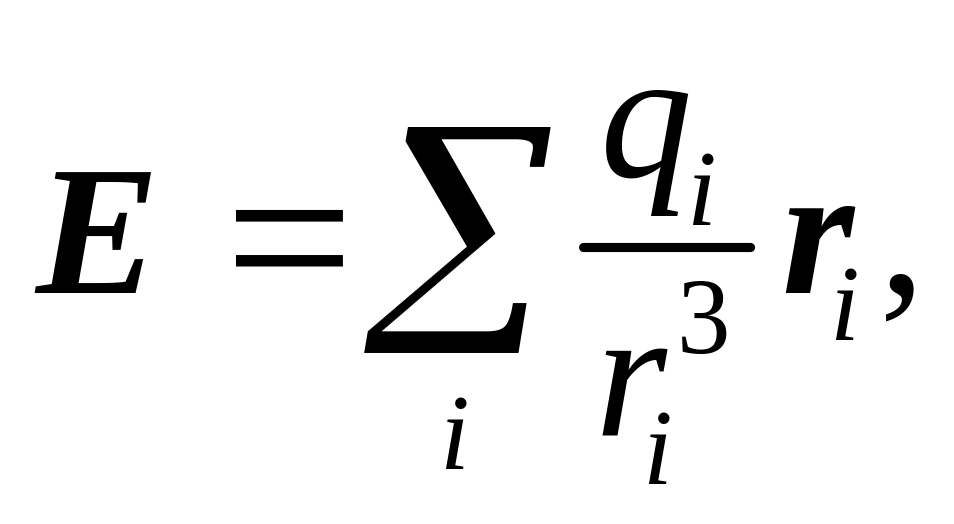
где r_i – радиус-вектор, проведённый от i – го заряда в точку, где ищется вектор напряжённости поля E.

Как только найдено направление вектора E₀ в исходной точке, так здесь найдено направление касательной к силовой линии. Двигаясь вдоль этого направления, попадём, сделав малый шаг в соседнюю точку. Там вновь найдём направление вектора E, и вновь сделаем вдоль него малый шаг. Так можем найти всю силовую линию. Описанный алгоритм очень прост, но весьма неточен. Поэтому в данной программе применён более сложный, но и более точный метод. О нём подробно написано в разделе Алгоритм построения линий поля.

Нахождение эквипотенциальной поверхности производится также на основе принципа суперпозиции с учетом того, что потенциал системы точечных зарядов равен сумме потенциалов отдельных зарядов, создающих это поле:

.

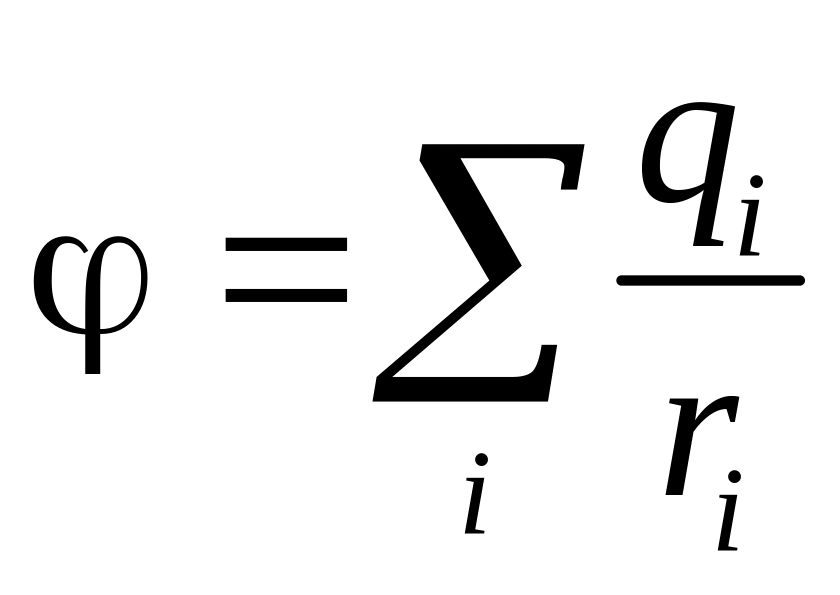Процедура нахождения эквипотенциальной поверхности реализуется следующим образом. В точке пространства, через которую мы хотим провести эквипотенциальную линию, вычисляется потенциал поля ₀, созданного системой зарядов и вектор напряжённости этого поля. Затем делаем из этой точки небольшой шаг в направлении, перпендикулярном вектору напряжённости поля. В новой точке, куда мы пришли, сделав небольшой шаг, вновь находим вектор напряжённости поля, и вновь делаем из этой точки небольшой шаг в направлении, перпендикулярном вектору напряжённости. Так можно отыскать все точки эквипотенциальной линии. Этот алгоритм также очень прост, но также весьма неточен. Поэтому в данной программе реализован более точный, но и значительно более сложный метод построения эквипотенциальных линий. Об этом методе также написано в разделе Алгоритм построения линий поля.