Приложение 2 Граничные условия для вектора плотности тока

Докажем справедливость утверждения об эквипотенциальности поверхности раздела проводников с сильно различающимися проводимостями. Рассмотрим ток, текущий через границу раздела двух проводящих сред с проводимостями ₁ и ₂. Вектор плотности тока в первой среде обозначим через j₁, а во второй – через j₂. При протекании постоянного тока количество зарядов, проходящих внутрь любой замкнутой поверхности, должно равняться нулю (заряды нигде не накапливаются). В частности, это справедливо для поверхности беско­нечно малого цилиндра, верхнее и нижнее основание которого параллельны границе раздела сред, а сами эти основания находятся по разные стороны границы раз дела (см. рис.1). Заряд dq₂, входящий в цилиндр через нижнее основание за время dt равен:

dq₂=j₂dScos₂dt (1),

а выходящий через верхнее основание за то же время:

dq₁=j₁dScos₁dt. (2)

Смысл углов 1 и 2 ясен из рис. 1. Если теперь неограниченно уменьшать высоту цилиндра, оставляя его верхнее основание в среде 1, а нижнее – в среде 2, то заряд, протекающий через боковую поверхность этого цилиндра, будет стремиться к нулю, и условие постоянства тока через границу запишется как: dq₁=dq₂.

Рис. 4

Откуда, учитывая (1) и (2), получим: j1 cos1 = j2cos2. (3) Поскольку в любой проводящей среде справедлив закон Ома: j=E, (4) то уравнение (3) можно записать в виде: 1E1cos1 = 2E2cos2. (5) Кроме того, на границе раздела двух сред выполняется соотношение: E1t = E2t, (6)

где Е_t – проекция вектора E, параллельная границе раздела двух сред. Поскольку, согласно (4), направления j и E совпадают, то уравнение (6) можно записать в виде:

E₁sin₁ = E₂sin₂. (7)

Поделив (7) на (5), получим:

,

или

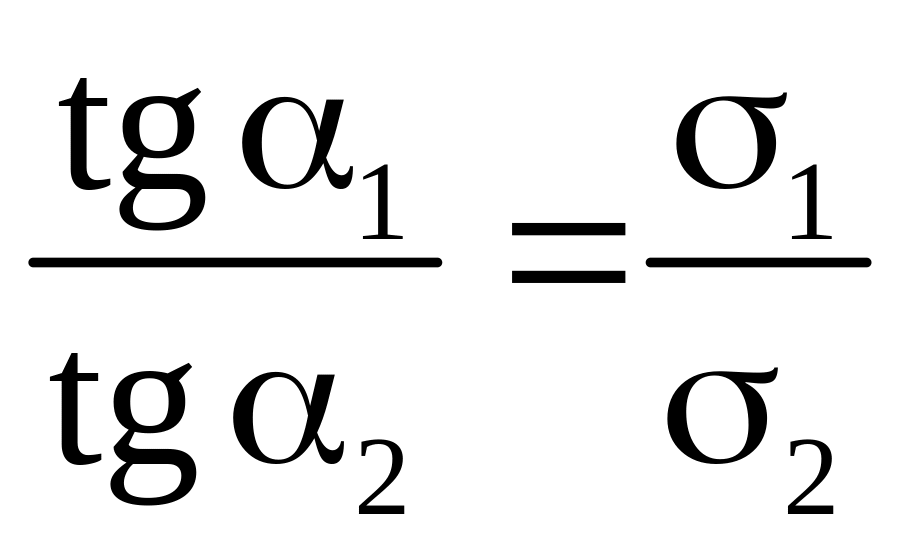. (8)

Если ₁  ₂, то tg₁, а вместе с ним угол ₁, будут малы, каков бы ни был ₂,:

. (9)

Это означает, что в случае контакта двух проводников с сильно различающимися проводимостями, электрический ток всегда течет практически перпендикулярно поверхности проводника с малой проводимостью (см. рис. 1). Поскольку, согласно (4), направление вектора напряженности поля совпадает с направлением плотности тока, то и вектор E в плохом проводнике практически перпен­дикулярен к его гра­нице, а это означает, что границу плохого и хорошего провод­ников можно считать эквипотенциальной поверхностью.

Далее, в силу закона сохранения заряда:

divj=0. (10)

Учитывая закон Ома (4) для случая однородной среды, получим ( = const в однородной среде):

divj = divE.

С учетом (10) получаем:

divE=0. (11)

Как видим, поле постоянного тока удовлетворяет такому же условию (11), что и поле в ва­кууме. Кроме того, поверхности электродов, создающих ток, эквипо­тенциальны, а это означает, что поле в проводящей среде совпадает с полем в вакууме, если оно создается такой же системой электродов, имеющих такие же потенциалы, что и электроды, создающие ток в среде.

Работа № 2 компьютерное моделирование электрических полей точечных зарядов

Цель работы:	Построить с помощью компьютера эквипотенциальные поверхности и силовые линии электростатического поля.
Приборы и принадлежности:	Персональный компьютер, принтер