
- •Озерский технологический институт – филиал нияу мифи
- •Оглавление
- •Предисловие
- •Методические указания
- •Работа № 1 изучение электростатического поля
- •Введение
- •Метод электролитической ванны
- •Порядок проведения работы установка 1
- •Установка 2
- •Контрольные вопросы
- •Приложение 1 Свойства силовых линий и эквипотенциальных поверхностей
- •Силовые линии начинаются и заканчиваются либо на зарядах, либо в бесконечности.
- •Густота силовых линий пропорциональна величине напряженности поля в данной области.
- •Приложение 2 Граничные условия для вектора плотности тока
- •Работа № 2 компьютерное моделирование электрических полей точечных зарядов
- •Введение
- •Выбор масштабов
- •Краткое описание алгоритма построения линий поля
- •Порядок работы как установить заряды и задать их параметры
- •Построение силовых линий и эквипотенциальных поверхностей
- •Электрический диполь:
- •Электрический квадруполь с зарядами:
- •Комментарии к заданию
- •Процедура печати
- •Контрольные вопросы
- •Работа 3 измерение ёмкости конденсатора
- •Введение
- •Методика измерения ёмкости конденсатора
- •Описание установки
- •Порядок проведения эксперимента
- •Контрольные вопросы
- •Литература
- •Приложение
- •Работа № 4 измерение температуры кюри сегнетоэлектрика
- •Введение
- •Описание установки и методика проведения измерений
- •Порядок выполнения работы
- •Контрольные вопросы
- •Работа №5 изучение гистерезиса сегнетоэлектрика
- •Введение
- •Описание установки
- •Назначение ист-2м
- •Наблюдение петли гистерезиса сегнетоэлектрика
- •Контрольные вопросы
- •Работа № 6 исследование цепи постоянного тока
- •Проверка закона ома для замкнутой цепи введение
- •Порядок выполнения работы
- •Изучение нелинейного элемента введение
- •Порядок выполнения работы
- •Контрольные вопросы
- •Работа № 7 измерение величины постоянного магнитного поля
- •Методика измерений и описание прибора
- •Порядок выполнения работы
- •Контрольные вопросы
- •Работа № 8 измерение магнитного поля постоянного магнита
- •Методика измерений и описание прибора
- •Порядок выполнения работы
- •Контрольные вопросы
- •Приложение
- •Работа № 9 измерение магнитной восприимчивости диа- и парамагнетиков
- •Введение
- •Порядок выполнения работы
- •Контрольные вопросы
- •Работа № 10 определение температуры кюри ферромагнетика
- •Введение
- •Метод определения температуры кюри
- •Приборы и принадлежности
- •Порядок выполнения работы
- •Контрольные вопросы
- •Работа № 11 изучение гистерезиса ферромагнетика
- •Введение
- •Описание установки
- •Порядок выполнения работы Задание 1. Снятие кривой намагничивания.
- •Задание 2. Определение коэрцитивной силы и остаточной намагниченности.
- •Задание 3. Оценка работы намагничивания за один цикл.
- •Контрольные вопросы.
- •Приложение Работа по перемагничиванию ферромагнетика
- •Работа № 12 измерение магнитной проницаемости ферромагнетика
- •Введение
- •Описание установки и методики измерений
- •Порядок выполнения работы:
- •Контрольные вопросы.
- •Работа № 13 измерение удельного заряда электрона
- •Введение
- •Описание установки
- •Порядок выполнения работы
- •Контрольные вопросы
- •Литература
- •Работа № 14 измерение удельного заряда электрона
- •1. Описание
- •2. Основные принципы
- •3. Предварительная настройка
- •4. Порядок измерений
- •Работа 15 измерение индуктивности катушки
- •Введение
- •Методика измерения индуктивности катушки
- •Описание установки
- •Порядок проведения эксперимента
- •Контрольные вопросы
- •Литература
- •Приложение
- •Работа № 16 резонанс в колебательном контуре
- •Введение
- •Методика измерений
- •Описание установки
- •Порядок проведения эксперимента
- •Контрольные вопросы
Через любую точку поля можно провести силовую линию, причем единственную. Это означает, в частности, что силовые линии не могут пересекаться друг с другом. Исключением из этого утверждения являются точки, в которых напряженность поля обращается в нуль (нулевому вектору можно приписать любое направление) или в бесконечность.
Силовые линии начинаются и заканчиваются либо на зарядах, либо в бесконечности.
Густота силовых линий пропорциональна величине напряженности поля в данной области.
Здесь надо иметь в виду, что именно так требуется изображать поле с помощью силовых линий. Поэтому доказывать тут вроде бы нечего. Однако, как мы сейчас убедимся, это требование вытекает из теоремы Гаусса, согласно которой поток вектора напряженности поля через любую замкнутую поверхность пропорционален заряду, находящемуся внутри области, ограниченной этой поверхностью. |
Рис. 1 |
Действительно, пусть в какой-либо точке поля вектор напряженности равен E1. Проведем через эту точку небольшую площадку площади S1, расположив ее перпендикулярно вектору E1. Проведем теперь через точки контура, ограничивающего площадку, силовые линии. Мы получим трубку силовых линий. Все те силовые линии, что оказались внутри трубки никогда за пределы трубки не выйдут (см. П. 1). Проведем еще один контур, охватывающий эту трубку, плоскость которого также перпендикулярна линиям, проходящим через точки этого контура. Пусть площадь, охватываемая этим контуром равна S2, а напряженность поля в этой области равна E2.
Мы получили замкнутую поверхность, внутри которой нет зарядов. Поток через поверхность трубки силовых линий, ограничивающих эту поверхность равен нулю. Напомним, что поток вектора Е через площадку площади dS равен (E,n)dS=EdScos, где - угол между Е и вектором нормали к площадке n (см. рис. 1). Если |
Рис. 2 |
замкнутая поверхность не содержит внутри себя зарядов, то поток вектора напряженности через такую поверхность будет равен нулю.
Поток вектора Е через площадку S1 отрицателен и равен –S1E1, а через вторую площадку поток равен S2E2 (напомним, что при вычислении потока через замкнутую поверхность необходимо выбирать внешнюю для этой поверхности нормаль; на рис. 2 это нормали n1 и n2). Поскольку внутри поверхности нет зарядов, то поток вектора Е через нее равен нулю:
S2E2–S1E1=0.
Следовательно, Е2/Е1=S1/S2. Поскольку число силовых линий N внутри трубки остается неизменным, то число силовых линий, проходящих через площадки S1 и S2 одинаково:
N1 =N2.
Густота линий – это количество линий, проходящих через площадку единичной площади, т.е. N/S. Тогда:
(N1/S1):(N2/S2)=S2/S1=E1/E2.
Итак, густота силовых линий пропорциональна напряженности поля в данной области, если только в ней нет зарядов.
Следует, однако, иметь в виду следующее обстоятельство. Силовую линию вы можете провести через любую точку поля, поэтому, сколько линий вы проведете в том или ином месте, зависит исключительно от вас. Следовательно, утверждение о пропорциональности густоты линий и напряженности поля можно применять к линиям, принадлежащим одной и той же трубке силовых линий. Т.е. оценивать напряженность поля в разных точках по густоте силовых линий можно лишь тогда, когда эти точки попадают внутрь одной и той же трубки силовых линий. Для разных трубок этого делать уже нельзя.
Силовые линии не могут касаться друг друга в точке, где нет зарядов. Это следствие п.п. 1 и3. Действительно, пусть две линии касаются друг друга в какой-либо точке. Тогда в точке касания двух линий густота этих линий будет бесконечной, т.е. напряженность поля в этой точке также будет бесконечной. Это невозможно, если только в этой точке нет заряда.
Рассмотрим теперь свойства эквипотенциальных поверхностей. Напомним, что эквипотенциальной поверхностью называется поверхность, все точки которой имеют один и тот же потенциал.
Для исследования свойств эквипотенциальных поверхностей необходимо помнить, что работа, которую совершает электрическое поле над единичным положительным зарядом при переносе его из точки 1 в точку 2, равна 1–2. Из этого определения сразу же следует:
Силовая линия направлена перпендикулярно эквипотенциальной поверхности в точке пересечения с нею. Действительно, пусть точки 1 и 2 находятся на одной и той же эквипотенциальной поверхности неподалеку друг от друга. Перенесем электрический заряд q вдоль эквипотенциальной поверхности из т.1 в т.2. Т.к. потенциалы в обеих точках одинаковы, то работа, совершаемая полем над зарядом равна нулю. Следовательно, сила, действующая на заряд F=qE, направлена перпендикулярно перемещению этого заряда. Т.к. заряд перемещался вдоль поверхности, то вектор E перпендикулярен поверхности.
Эквипотенциальные поверхности не могут пересекаться друг с другом в точке, где напряженность поля не равна нулю. Действительно, пересечение поверхностей означало бы, что в точках пересечения вектор напряженности поля имеет одновременно два различных направления, перпендикулярно как первой, так и второй поверхности. Это, очевидно, невозможно, если только в этих точках напряженность поля не равна нулю.
Поскольку потенциал и напряженность поля связаны соотношением:
![]()
где Es – проекция вектора E на направление вектора s, а производная d/ds означает производную от потенциала вдоль направления вектора s.
Последнее соотношение означает:
Густота эквипотенциальных поверхностей пропорциональна величине напряженности электрического поля в данной области. Действительно,
пусть имеем пару эквипотенциальных поверхностей, потенциалы которых равны, соответственно, 1 и 2. Пусть расстояние между поверхностями в какой-либо области равно s1, а в некоторой другой – s2. Тогда величину напряженности поля в первой области можно оценить как /s1, а во второй как /s2. |
|
Здесь мы символом обозначили разность потенциалов 2–1 между этими поверхностями. Ясно, что чем меньше расстояние между поверхностями, тем выше напряженность поля в данной области.
Применение этого утверждения ограничено областью между парой заданных поверхностей. В какой-либо области вне данной пары оценить так напряженность поля уже нельзя. Дело опять-таки в том, что через любую точку поля вы можете провести эквипотенциальную поверхность. И хотя принято изображать эквипотенциальные поверхности с равным шагом по потенциалу, но, сколько вы их проведете внутри какой-либо области, зависит исключительно от вас. Все это очень похоже на аналогичное утверждение о связи густоты силовых линий и напряженности поля.


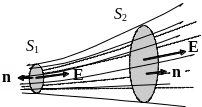
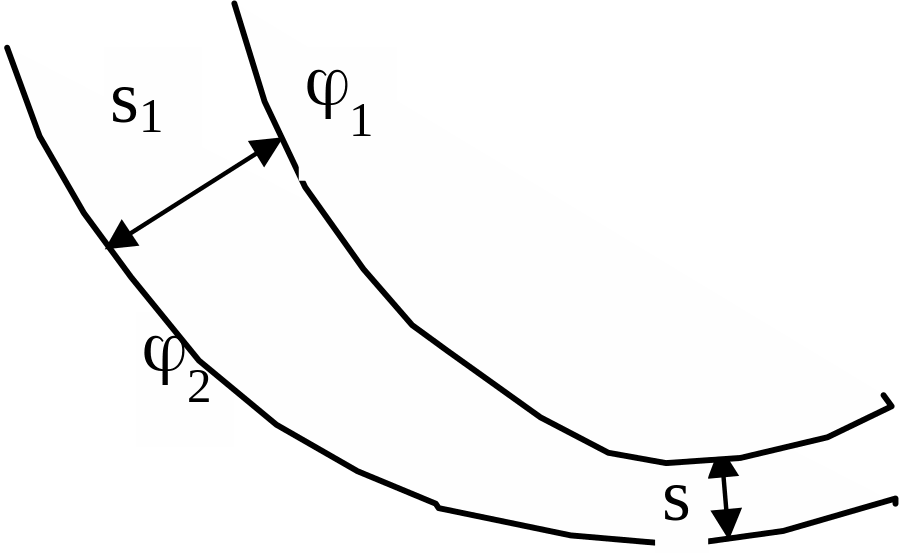 Рис.
3
Рис.
3