Литература

1. Элементарный учебник физики под ред. академика Г.С. Ландсберга. Т.2.

2. И.В. Савельев. Курс общей физики. Т.2.

3. Д.В. Сивухин. Общий курс физики. Т.3.

Приложение

Ток в RC цепи

Рис. П1

Пусть к источнику переменного напряжения последовательно подключены конденсатор и резистор (проводник, обладающий заметным сопротивлением). Тогда в цепи появится ток. В любой момент времени сумма напряжений на резисторе и конденсаторе равна напряжению на источнике:

Разделим обе части этого уравнения на R, тогда получим:

(П1)

Решение этого уравнения зависит от вида правой части. В дальнейшем нас будет интересовать только случай, когда напряжение изменяется по гармоническому закону, т.е. U = U₀ cost. Тогда и заряд на конденсаторе будет колебаться с той же частотой, но, вообще говоря, с другой фазой:

q = q₀ cos(t + ). (П2)

Как видим, решение задачи сводится к отысканию двух величин:

q₀ и .

Для их нахождения подставим выражение (П2) в (П1) и получим следующее уравнение:

Это уравнение нетрудно решить. Действительно, обозначив для краткости

a=1/RC, b=,

а затем, умножив и разделив выражение в скобках на сумму квадратов коэффициентов при синусе и косинусе, получим:

Заметим, что коэффициенты при синусе и косинусе меньше единицы, а сумма их квадратов равна единице. Поэтому можно ввести обозначения:

В результате получим:

Полученное равенство должно быть справедливо при любых t, поэтому:

Амплитуда напряжения на резисторе U=RI₀:

Построим график зависимости U/U₀ от , для чего преобразуем полученную формулу, введя обозначение:

=RC.

Тогда эта формула запишется в виде:

(П3),

Как видим, при 0 U  0, а при  U  U₀, т.е. график асимптотически приближается к прямой U/U₀ = 1.

График зависимости U/U₀ от  (он называется амплитудно-частотной характеристикой, или коротко – АЧХ) изображён на рисунке П2.

Заметим, что начальный участок графика, соответствующий малым значениям  (<<1, т.е.  << 1/RC), является линейным:

Поэтому при малых частотах, когда <<1:

Рис. П2

В обратном случае высоких частот, таких, что  >> 1/RC, напряжение на резисторе остаётся неизменным, равным напряжению на выходе генератора:

U=U₀.

Эти предельные случаи, как было показано раньше, можно получить практически без математики.

Работа № 4 измерение температуры кюри сегнетоэлектрика

Цель работы:	Получить зависимость диэлектрической проницаемости от температуры и определить точку Кюри в сегнетоэлектрике.
Приборы и принадлежности:	Термопара, милливольтметр для измерения термоэдс термопары, микроамперметр, вольтметр, нагреватель, трансформатор, градуировочная кривая термопары.

Введение

Молекулы всякого диэлектрического тела, помещенного в электрическое поле, поляризуются, т.е. приобретают дипольный момент. Сумма дипольных моментов молекул в единице объема называется вектором поляризации (другое название – поляризованность). В большинстве диэлектриков вектор поляризации P связан линейным соотношением с напряженностью электрического поля в диэлектрике E:

P=₀E, (1)

где  – электрическая восприимчивость диэлектрика, ₀=0,88510^-11ф/м – электрическая постоянная.

Однако, существует класс кристаллических диэлектриков, поляризованность которых отлична от нуля и в отсутствие электрического поля. Такие диэлектрики, обладающие спонтанной (самопроизвольной) поляризованностью называются сегнетоэлектриками. Величина вектора спонтанной поляризации сегнетоэлектрика зависит от температуры. С повышением температуры она уменьшается и при достижении сегнетоэлектриком определенной температуры Т_с, называемой температурой Кюри, спонтанная поляризованность исчезает. Спонтанная поляризованность в сегнетоэлектриках обычно не бывает однородной, т.е. в кристалле возникает ряд областей (чаще всего слоев) с различными направлениями поляризованности. Возникновение таких областей, называемых доменами, объясняется тем, что состояние кристалла со многими доменами оказывается энергетически более выгодным, то есть обладает меньшей энергией, нежели состояние, когда весь кристалл представляет собой один домен. При этом дипольный момент кристалла в целом оказывается равным нулю. Наличие доменов в сегнетоэлектриках приводит к тому, что величина вектора поляризации кристалла P неоднозначно зависит от величины электрического поля E в кристалле (см. рис. 1). Объясняется эта зависимость тем, что изменение поляризованности сегнетоэлектрика при увеличении напряженности электрического поля связано с изменением размеров доменов. Те домены, в которых угол между векторами P и E острый – растут, другие, в которых этот угол тупой, – уменьшаются.

Этот процесс носит необратимый характер, поэтому при снятии внешнего поля кристалл остается поляризованным. Величина этой поляризованности носит название остаточной. Чтобы полностью уничтожить поляризованность, необходимо создать в кристалле поле противоположного направления по сравнению с направлением поляризованности. Величина этого поля Ес носит название коэрцитивной силы. Зависимость Р от Е, изображенная на рис. 1, называется петлей гистерезиса.

Рис. 1

Диэлектрическая проницаемость сегнетоэлектрика оказывается очень большой (~10³–10⁴), кроме того, она зависит от температуры. Вблизи температуры Кюри диэлектрическая проницаемость сегнетоэлектрика зависит от температуры по закону Кюри:

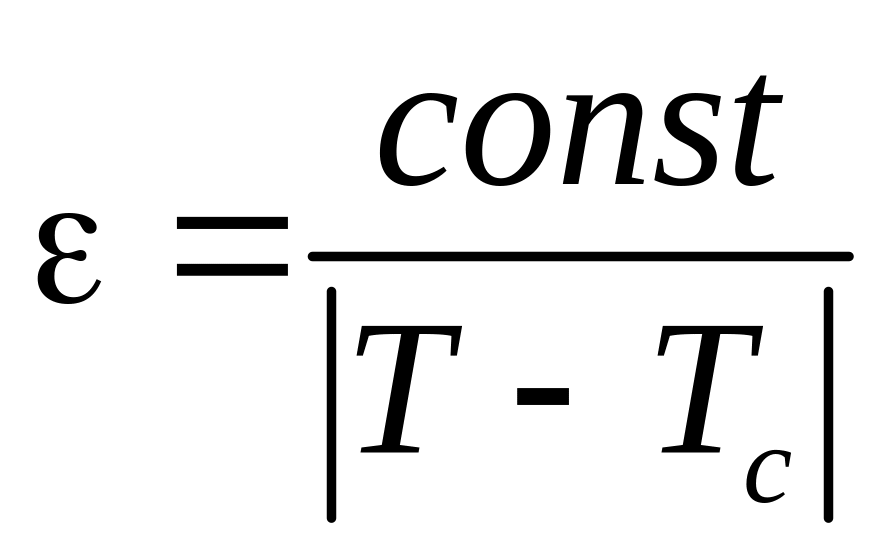, (2)

обращаясь в бесконечность при T = T_c (см. Рис 2а).

В (2) значение const при T<T_c отличается от ее значения при T>T_c.

Заметим, что , т.е. эта величина обращается в нуль в точке Кюри. При этом вблизи температуры Кюри график зависимости 1/ от температуры линеен (см. рис. 2б).

Отметим, что переход диэлектрика из сегнетоэлектрического состояния в несегнетоэлектрическое является фазовым переходом, в котором происходит изменение структуры кристаллической решетки.