Занятие №7. Теория игр План занятия:

1. Организационный момент.

2. Объяснение нового материала.

3.Усвоение и закрепление нового материала. Решение практических заданий

№1.

Показать, что игра заданная следующей платежной матрицей, имеет решение в чистых стратегиях. Найти ее решение.

Решение.

Найдем нижнюю и верхнюю цену игры:

a_ij = max{минимальные элементы строчек} = max{-3, 5, -9} = 5;

a_ij = min{максимальные элементы столбцов} = min{8, 5, 9, 8} = 5.

Таким образом, a_ij = a_ij = a₂₂=5. Платежная матрица имеет седловую точку (2, 2). Цена игры a₀=a₂₂=5. Оптимальные стратегии: для первого игрока – вторая и для второго – вторая.

В №2-№5 решить матричную игру, заданную платежной матрицей:

№ 2.

а) 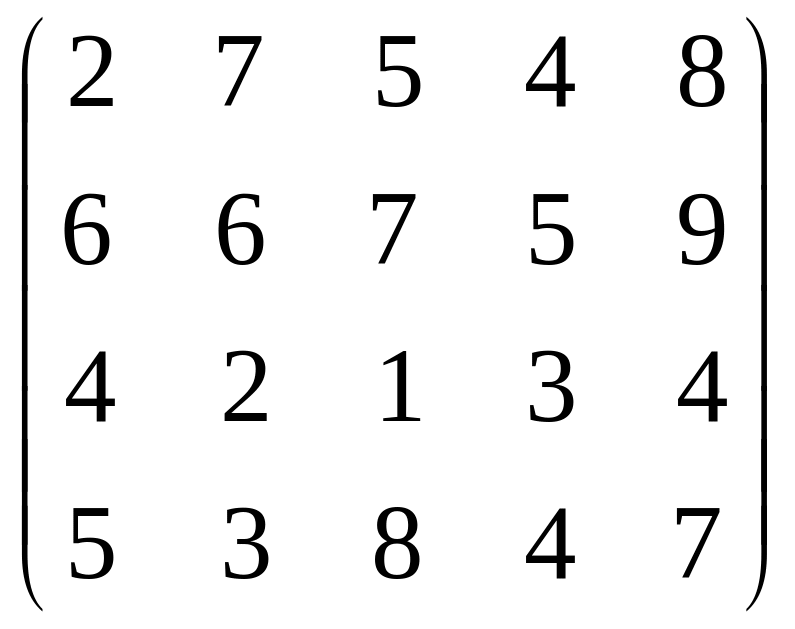б)

№ 3.

а) б)

№ 4.

а) б)

№ 5.

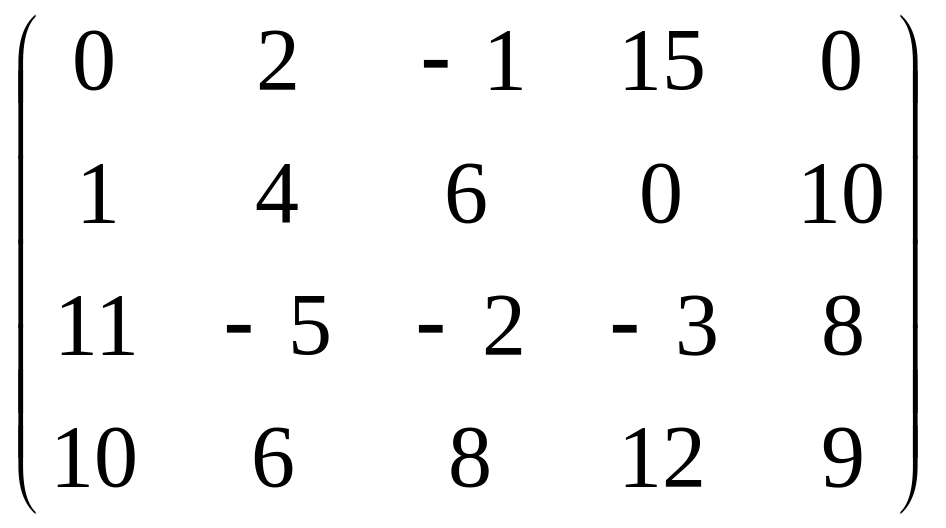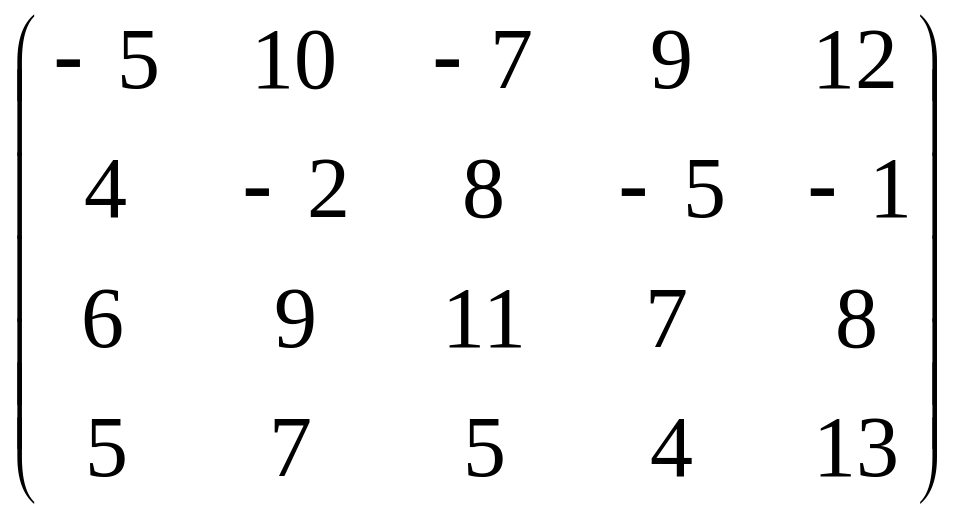а) б)

4. Подведение итогов занятия.

5. Постановка домашнего задания.