
- •Практические занятия Занятие №1. Метод Жордана-Гаусса решения систем линейных уравнений План занятия:
- •Решение практических заданий
- •Занятие №2. Понятие задачи линейногопрограммирования План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала:
- •3.Усвоение и закрепление нового материала. Решение практических заданий
- •Занятие №3. Геометрический метод решения задач линейного программирования План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала:
- •3.Усвоение и закрепление нового материала. Решение практических заданий
- •Занятие №4. Симплексный метод План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала:
- •3.Усвоение и закрепление нового материала. Решение практических заданий
- •Занятие №5. Двойственные задачи линейного программирования План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала:
- •3.Усвоение и закрепление нового материала. Решение практических заданий
- •Занятие №6. Транспортная задача линейного программирования План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала:
- •3.Усвоение и закрепление нового материала. Решение практических заданий
- •Занятие №7. Теория игр План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала.
- •3.Усвоение и закрепление нового материала. Решение практических заданий
Занятие №6. Транспортная задача линейного программирования План занятия:
1. Организационный момент.
2. Объяснение нового материала:
1.Открытая и закрытая модели транспортной задачи. Переход к закрытой модели. Математическая модель транспортной задачи и ее особенности.
2.Теорема о существовании решения транспортной задачи. Ранг транспортной задачи. Методы первоначального распределения поставок.
3.Потенциалы поставщиков и потребителей. Нахождение потенциалов. Оценка клетки и матрица оценок клеток. Критерий оптимальности для транспортной задачи.
4.Понятие цикла клетки. Существование и единственность цикла клетки. Построение цикла клетки. Перераспределение поставок по циклу.
5.Алгоритм решения транспортной задачи.
3.Усвоение и закрепление нового материала. Решение практических заданий
№1. Решить транспортную задачу, исходные данные которой таковы:
bj ai |
200 |
200 |
300 |
400 |
200 |
4 |
3 |
2 |
1 |
300 |
2 |
3 |
5 |
6 |
500 |
6 |
7 |
9 |
12 |
Решение.
1. Проверяем выполнение необходимого и достаточного условия разрешимости задачи. Находим суммарные запасы поставщиков и суммарные запросы потребителей:
![]()
Задача с неправильным балансом. Вводим
четвертого, фиктивного поставщика с
запасами
![]() и нулевыми стоимостями единиц груза.
и нулевыми стоимостями единиц груза.
2. Находим начальное опорное решение
методом минимальной стоимости. Полученное
решение
имеет
![]() базисных переменных. Вычисляем значение
целевой функции на этом опорном решении:
базисных переменных. Вычисляем значение
целевой функции на этом опорном решении:
![]() .
.
bj ai |
200 |
200 |
300 |
400 |
200 |
4 |
3 |
2 |
1 200 |
300 |
2 200 |
3 100 |
5 |
6 |
500 |
6 |
7 100 |
9 300 |
12 100 |
100 |
0 |
0 |
0 |
0 100 |
3. Для проверки оптимального опорного
решения необходимо найти потенциалы.
По признаку оптимальности в каждой
занятой опорным решением клетке таблицы
транспортной задачи сумма потенциалов
равна стоимости
![]() .
Записываем систему уравнений для
нахождения потенциалов и решаем ее:
.
Записываем систему уравнений для
нахождения потенциалов и решаем ее:
![]()
Система состоит из семи уравнений и
имеет восемь переменных. Система
неопределенная. Одному из потенциалов
задаем значение произвольно: пусть
![]() .
.
Остальные потенциалы находятся однозначно:
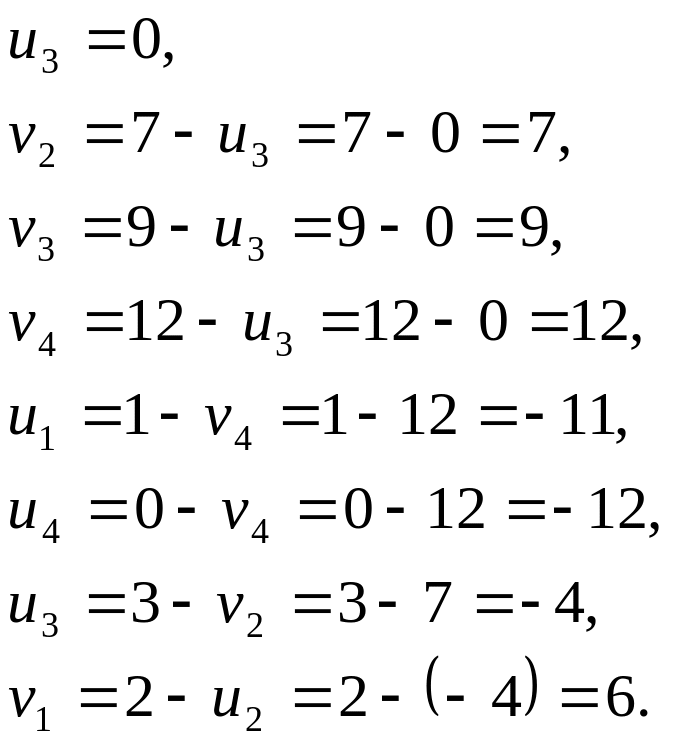
Значения потенциалов записываем в таблицу рядом с запасами или запросами соответствующих поставщиков и потребителей.
Система уравнений для нахождения потенциалов достаточно проста, обычно ее решают устно. Любой неизвестный потенциал, соответствующий занятой клетке, равен находящейся в этой клетке стоимости минус известный потенциал, соответствующий этой же клетке.
4. Проверяем опорное решение
на оптимальность. С этой целью вычисляем
оценки
![]() для всех незаполненных клеток таблицы
(для всех занятых клеток
для всех незаполненных клеток таблицы
(для всех занятых клеток
![]() ):
):
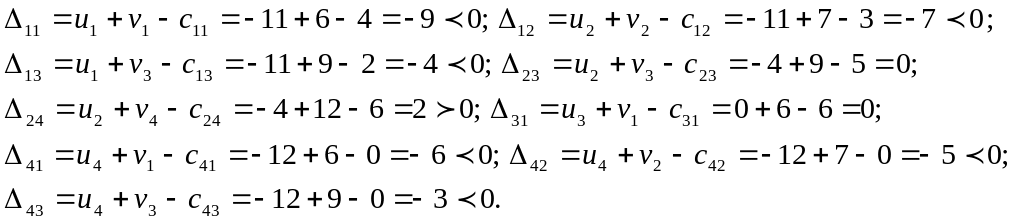
Положительные оценки записываем в левые нижние углы соответствующих клеток таблицы, вместо отрицательных ставим «-».
Начальное опорное решение не является
оптимальным, так как имеется положительная
оценка
![]()
5. Переходим к новому опорному решению.
Для клеток
![]() с положительной оценкой строим цикл.
Ставим в эту клетку знак «+», присоединяем
ее к занятым клеткам и, применяя метод
вычеркивания, находим цикл
с положительной оценкой строим цикл.
Ставим в эту клетку знак «+», присоединяем
ее к занятым клеткам и, применяя метод
вычеркивания, находим цикл
![]() .
В угловых точках цикла расставляем
поочередно знаки «+» и «-», начиная с «+»
в клетке
.
В клетки, отмеченные знаком «+», добавляем
груз
.
В угловых точках цикла расставляем
поочередно знаки «+» и «-», начиная с «+»
в клетке
.
В клетки, отмеченные знаком «+», добавляем
груз
![]() ,
а из клеток, отмеченных знаком «-»,
убавляется такой же по величине груз.
Определяем величину груза
,
перераспределяемого по циклу. Она равна
значению наименьшей из перевозок в
клетках цикла, отмеченных знаком
,
а из клеток, отмеченных знаком «-»,
убавляется такой же по величине груз.
Определяем величину груза
,
перераспределяемого по циклу. Она равна
значению наименьшей из перевозок в
клетках цикла, отмеченных знаком
«-»:![]() .
Осуществляем сдвиг по циклу на величину
.
Осуществляем сдвиг по циклу на величину
![]() .
Получаем второе опорное решение
.
Получаем второе опорное решение
![]() .
.
bj ai |
200 |
200 |
300 |
400 |
200 |
4 |
3 |
2 |
1 200 |
300 |
2 200 |
3
|
5 |
6 100 |
500 |
6 |
7 200 |
9 300 |
12
|
100 |
0 |
0 |
0 |
0 100 |
Находим для этого решения потенциалы. Вычисляем оценки:
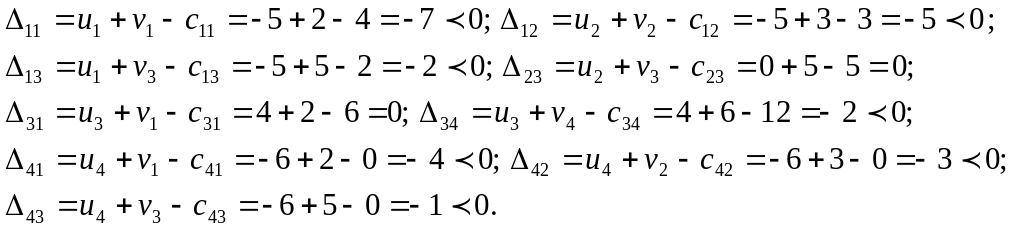
Все оценки неположительные. Следовательно, решение является оптимальным. Вычисляем значение целевой функции на этом решении:
![]() .
.
Ответ:
![]() .
.
В №2-№7 дана транспортная задача.
Необходимо:
1) составить экономико-математическую модель задачи;
2) выполнив первоначальное распределение указанным методом, найти
оптимальное распределение поставок
2. A=(30, 40, 20); 3. A=(30, 50, 20, 20) 4. A=(100, 250,200)
B=(30, 20, 30) B=(50, 10, 20) B=(180, 220, 100, 100)
C
=
 C
=
C
=
 C
=
C
=
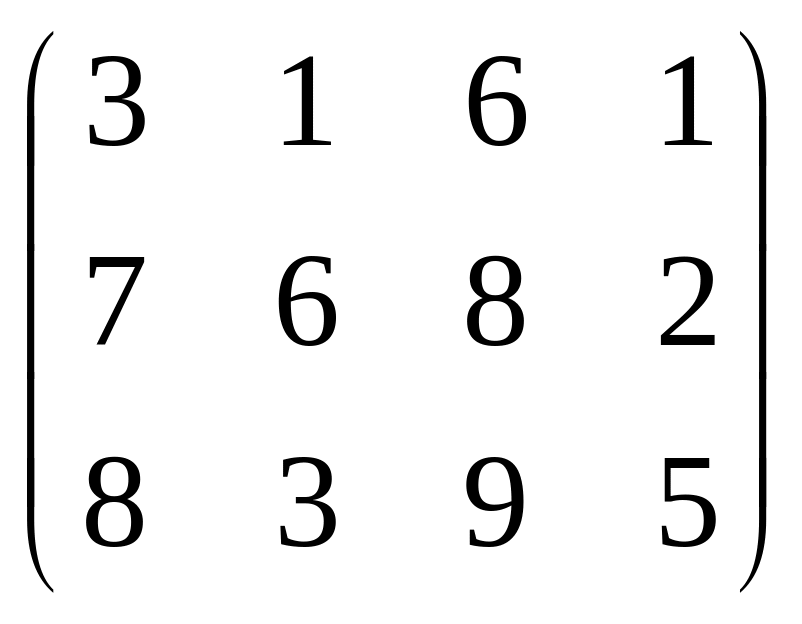
метод северо-западного угла метод наименьших затрат метод наименьших затрат
5.A=(34, 27, 18); 6. A=(100, 180, 120) 7. A=(45, 45, 50)
B=(21, 26, 27, 22) B=(80, 150, 70) B=(25, 25, 40, 60)
C
=
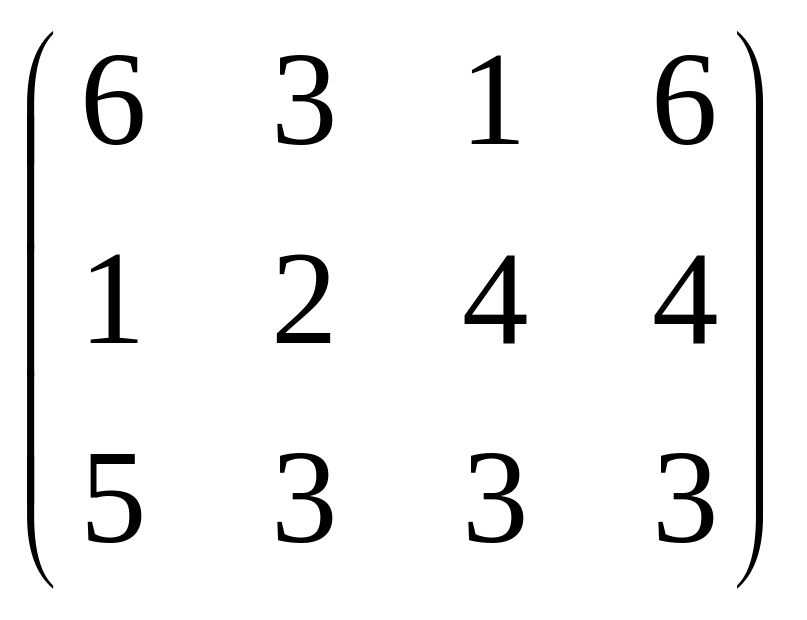 C
=
C
=
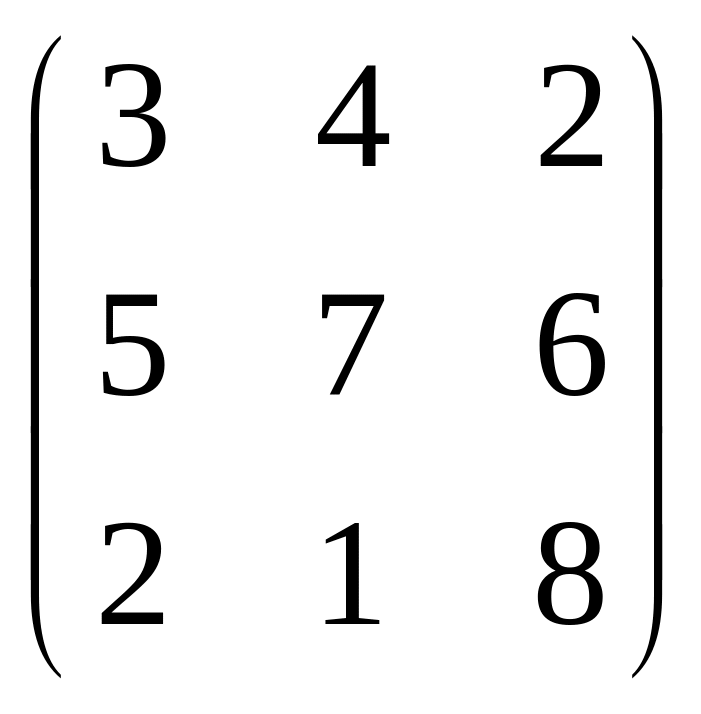 C
=
C
=

метод северо-западного угла метод наименьших затрат метод наименьших затрат
4. Подведение итогов занятия.
5. Постановка домашнего задания.
