Занятие №4. Симплексный метод План занятия:

1. Организационный момент.

2. Объяснение нового материала:

1.Общая постановка задачи линейного программирования. Представление задачи линейного программирования в каноническом, стандартном и симплексном видах. Эквивалентность этих представлений

2.Критерий оптимального решения задачи линейного программирования. Алгоритм решения задачи линейного программирования симплексным методом. Критерий единственности решения задачи линейного программирования.

3.Усвоение и закрепление нового материала. Решение практических заданий

№1. Решить симплексным методом:

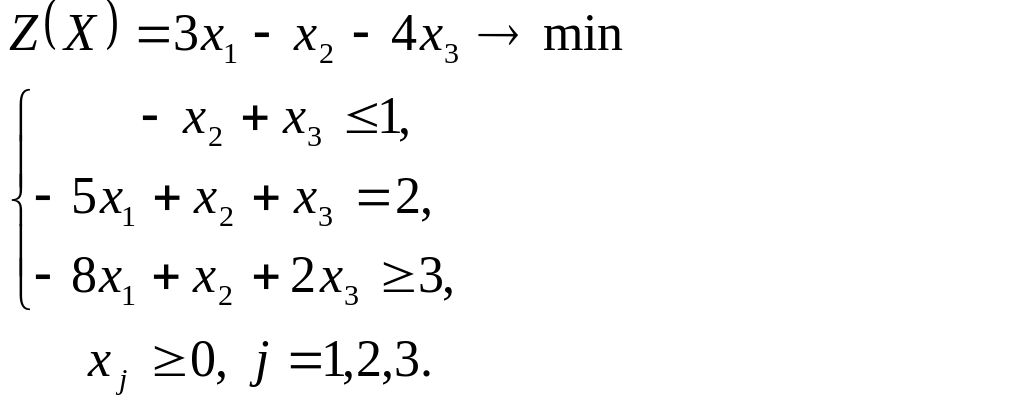
Решение.

Приводим задачу к каноническому виду:

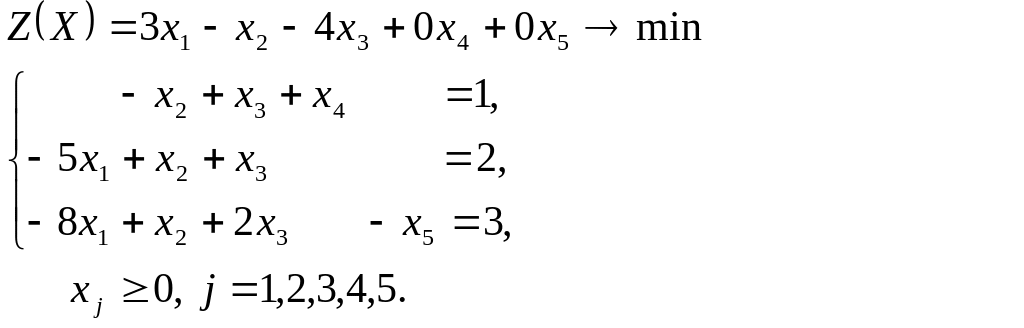
Используя метод Жордана-Гаусса, приведем систему ограничений задачи к равносильной разрешенной системе уравнений. При этом, используя параметр Q_k, сохраним правые части уравнений неотрицательными. Получим начальное опорное решение с базисом . Затем вычислим оценки расположений векторов условий по базису опорного решения и дополним таблицу расчета строкой оценок.

3 -1 -4 0 0

Б	Сб		A0	A1 A2 A3 A4 A5	Q1	Q2	Q3	Q4
Нахождение начального опорного решения			1 2 3	0 -1 1 1 0 -5 1 1 0 0 -8 1 2 0 -1	- - -	- 2 3	1 2 3/2	- - -
			3 2 1	-5 0 2 1 0 -5 1 1 0 0 -3 0 1 0 -1	- - -	- - -	3/2 2 1	- - -
A4 A2 A3		0 -1 -4	1 1 1	1 0 0 1 2 -2 1 0 0 1 -3 0 1 0 -1	1 - -	- - -	- - -	1/2 1 -
			-5	11 0 0 0 3
A1 A2 A3		3 -1 -4	1 3 4	1 0 0 1 2 0 1 0 2 5 0 0 1 4 3
			-16	0 0 0 -11 -19

Начальное опорное решение не является оптимальным, так как векторам соответствуют положительные оценки. По признаку оптимальности в задаче на минимум все оценки должны быть неположительными. Определяем, введение какого из векторов ( ) в базис приведет к большему уменьшению целевой функции:

.

В базис вводим вектор . Исключаем из базиса вектор , соответствующий минимуму параметра Q₀₁=1 при l=1. Выполняем преобразование Жордана-Гаусса, получаем второе опорное решение с базисом . Данное опорное решение является оптимальным, потому что оценки для всех векторов условий неположительные. Оптимальное решение единственное, так как векторы, не входящие в базис, не имеют нулевых оценок.

Ответ: .

Задачи №2-№4 представить в каноническом, стандартном и симплексном видах и решить симплексным методом:

№2. Предприятие выпускает продукцию двух видов A и B, используя три вида ресурсов. Запасы ресурсов, нормы их расхода и прибыль от реализации единицы продукции приведены в таблице. Определить план производства продукции, обеспечивающий наибольшую прибыль.

1.

Ресурсы	Нормы расхода сырья на единицу продукции		Запасы ресурсов
	A	B
Трудовые	12	15	360
Оборудование	6	4	240
Сырье	5	3	180
Прибыль	9	10

2.

Ресурсы	Нормы расхода сырья на единицу продукции		Запасы ресурсов
	A	B
Трудовые	8	6	240
Оборудование	5	6	300
Сырье	4	7	180
Прибыль	8	12

3.

Ресурсы	Нормы расхода сырья на единицу продукции		Запасы ресурсов
	A	B
Трудовые	15	12	330
Оборудование	4	5	240
Сырье	5	6	300
Прибыль	6	9

4.

Ресурсы	Нормы расхода сырья на единицу продукции		Запасы ресурсов
	A	B
Трудовые	7	5	350
Оборудование	2	4	280
Сырье	3	5	180
Прибыль	8	10

5.

Ресурсы	Нормы расхода сырья на единицу продукции		Запасы ресурсов
	A	B
Трудовые	5	6	180
Оборудование	8	4	240
Сырье	4	3	120
Прибыль	9	7

№3. Предприятие может производить изделие двумя технологическими способами, используя три вида ресурсов. Запасы ресурсов и нормы их расхода приведены в таблице. Определить план производства продукции, обеспечивающий наибольший валовой выпуск.

1.

Ресурсы	Нормы расхода сырья на единицу продукции		Запасы ресурсов
	I способом	II способом
Трудовые	2	1	60
Оборудование	5	4	250
Сырье	4	3	180

2.

Ресурсы	Нормы расхода сырья на единицу продукции		Запасы ресурсов
	I способом	II способом
Трудовые	1	5	90
Оборудование	2	2	140
Сырье	6	3	120

3.

Ресурсы	Нормы расхода сырья на единицу продукции		Запасы ресурсов
	I способом	II способом
Трудовые	2	5	160
Оборудование	1	1	80
Сырье	5	9	180

4.

Ресурсы	Нормы расхода сырья на единицу продукции		Запасы ресурсов
	I способом	II способом
Трудовые	3	7	210
Оборудование	1	4	80
Сырье	3	3	120

5.

Ресурсы	Нормы расхода сырья на единицу продукции		Запасы ресурсов
	I способом	II способом
Трудовые	6	9	270
Оборудование	2	5	150
Сырье	2	6	180

№4. Из двух веществ A и B, содержащих элементы K₁, K₂ и K₃, необходимо составить смесь. Количество этих элементов, содержащихся в единице веса каждого вещества, и стоимость единицы вещества приведены в таблице. Содержание элементов в смеси не должно быть меньше указанных объемов. Определить наиболее дешевый план закупки веществ.

1.

Элементы	Содержание элементов в 1 ед. веса вещества		Содержание элементов в смеси (не меньше)
	A	B
K1	4	6	36
K2	1	4	12
K3	4	2	16
Цена ед. веса вещества	4	5

2.

Элементы	Содержание элементов в 1 ед. веса вещества		Содержание элементов в смеси (не меньше)
	A	B
K1	5	8	40
K2	2	3	12
K3	2	5	10
Цена ед. веса вещества	3	4

3.

Элементы	Содержание элементов в 1 ед. веса вещества		Содержание элементов в смеси (не меньше)
	A	B
K1	1	3	9
K2	3	3	12
K3	2	1	10
Цена ед. веса вещества	2	4

4.

Элементы	Содержание элементов в 1 ед. веса вещества		Содержание элементов в смеси (не меньше)
	A	B
K1	2	2	14
K2	1	3	9
K3	3	0	18
Цена ед. веса вещества	4	2

5.

Элементы	Содержание элементов в 1 ед. веса вещества		Содержание элементов в смеси (не меньше)
	A	B
K1	5	1	15
K2	3	2	18
K3	4	5	20
Цена ед. веса вещества	3	3

4. Подведение итогов занятия.

5. Постановка домашнего задания.