
- •Практические занятия Занятие №1. Метод Жордана-Гаусса решения систем линейных уравнений План занятия:
- •Решение практических заданий
- •Занятие №2. Понятие задачи линейногопрограммирования План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала:
- •3.Усвоение и закрепление нового материала. Решение практических заданий
- •Занятие №3. Геометрический метод решения задач линейного программирования План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала:
- •3.Усвоение и закрепление нового материала. Решение практических заданий
- •Занятие №4. Симплексный метод План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала:
- •3.Усвоение и закрепление нового материала. Решение практических заданий
- •Занятие №5. Двойственные задачи линейного программирования План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала:
- •3.Усвоение и закрепление нового материала. Решение практических заданий
- •Занятие №6. Транспортная задача линейного программирования План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала:
- •3.Усвоение и закрепление нового материала. Решение практических заданий
- •Занятие №7. Теория игр План занятия:
- •1. Организационный момент.
- •2. Объяснение нового материала.
- •3.Усвоение и закрепление нового материала. Решение практических заданий
Занятие №3. Геометрический метод решения задач линейного программирования План занятия:
1. Организационный момент.
2. Объяснение нового материала:
Система координат на плоскости. Координаты точки. Нахождение координат точки. Построение точки по ее координатам.
Уравнение прямой. Уравнение прямой по двум точкам. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой. Условия пересечения, параллельности и совпадения двух прямых. Построение прямой, заданной общим уравнением.
Полуплоскости. Задание полуплоскостей. Изменение уравнения прямой при ее параллельном смещении.
Геометрический метод решения задач линейного программирования.
3.Усвоение и закрепление нового материала. Решение практических заданий
№1.
Решить задачу линейного программирования геометрическим методом:
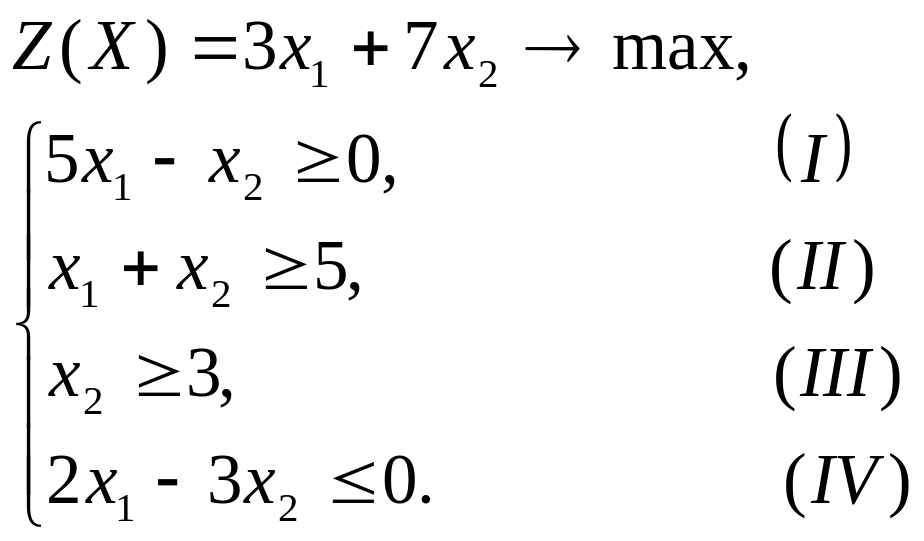
Решение.
Этап 1. Строим область допустимых решений. Для этого в системе координат Ox1x2 строим прямые: 5x1-x2=0; x1+x2=5; x2=3; 2x1-3x2=0. Ни одна из этих прямых не проходит через точку (1,0). Выберем ее в качестве контрольной точки. Подставляем координаты контрольной точки в систему основных ограничений. Получим систему числовых неравенств: 50, 15, 13, 20. Из этих неравенств следует, что полуплоскостью решений первого неравенства является полуплоскость, содержащая точку (1,0). А полуплоскостями решений остальных неравенств – полуплоскости, не содержащие контрольную точку. Общая часть полуплоскостей решений четырех неравенств является областью допустимых решений, На рисунке это открытый многоугольник ABC.

Этап 2. Строим линии уровня Z=21
и Z=42. Вектор
![]() направленный от Z=21
к Z=42 указывает
направление роста значений целевой
функции. В виду того, что в этом направлении
область допустимых решений не ограничена,
линия уровня уходит в бесконечность.
Следовательно,
направленный от Z=21
к Z=42 указывает
направление роста значений целевой
функции. В виду того, что в этом направлении
область допустимых решений не ограничена,
линия уровня уходит в бесконечность.
Следовательно,
![]() и задача не имеет конечного решения.
и задача не имеет конечного решения.
Задачи №2-№7 линейного программирования решить геометрическим методом:
2. Найти максимум функции 3. Найти минимум функции
F = 2x1 + 3x2 при ограничениях F = -2x1 + 3x2 при ограничениях
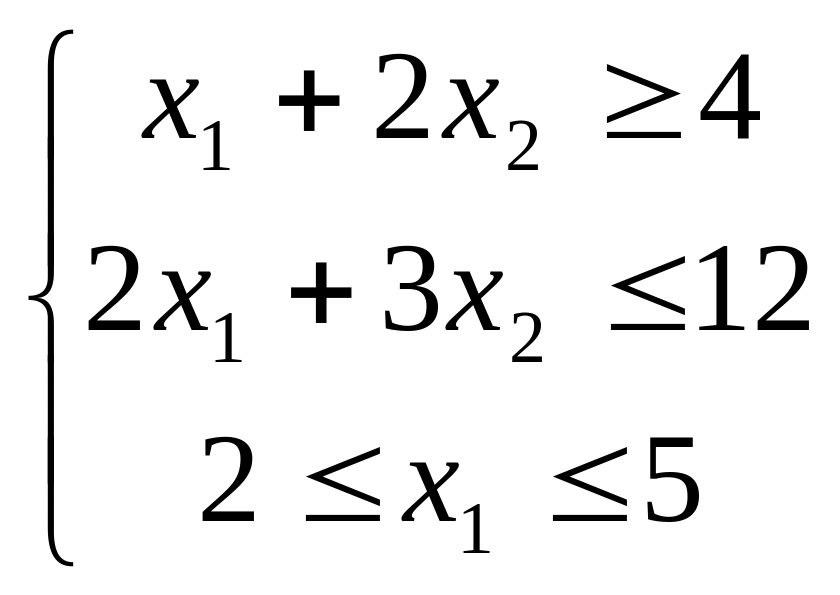
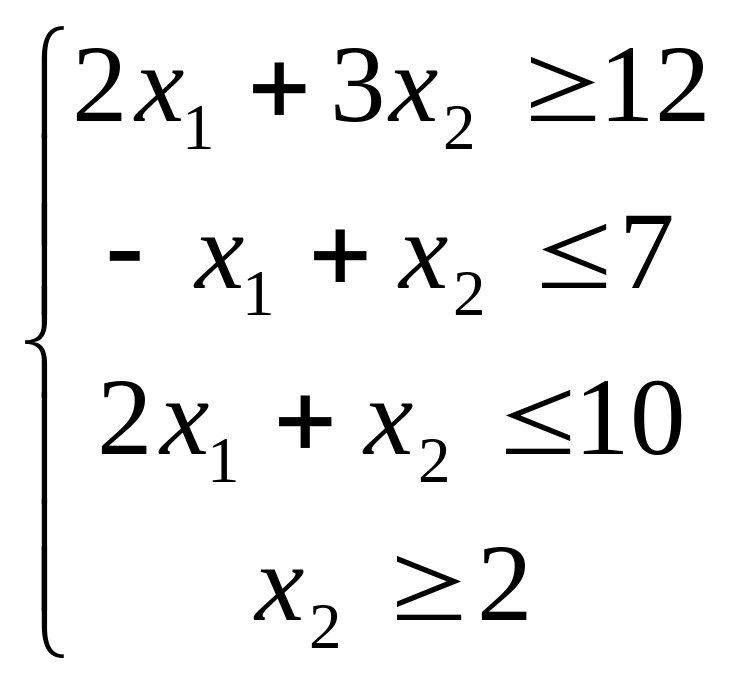
x1≥0,
x2≥0.
![]()
4. Найти максимум функции 5. Найти минимум функции
F = 3x1 + 3x2 при ограничениях F = 3x1 - 2x2 при ограничениях
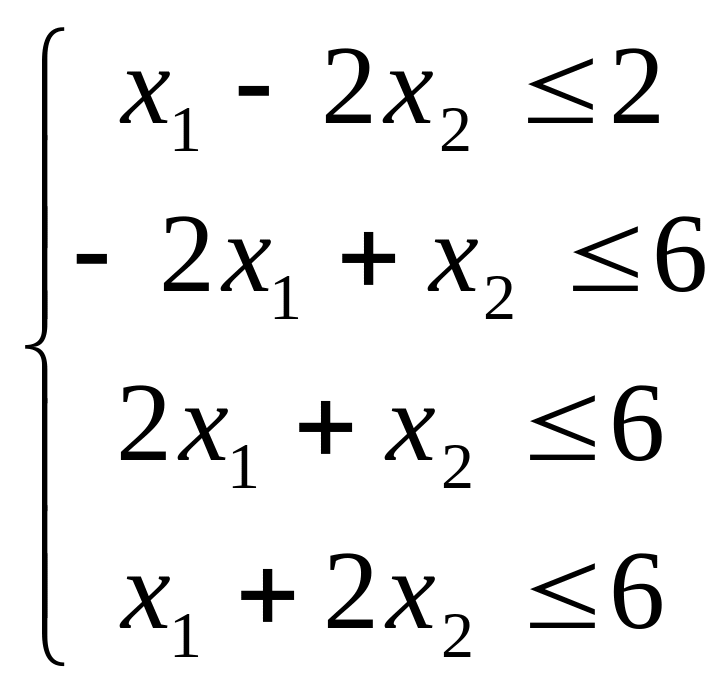

x1≥0, x2≥0.
6. Найти максимум функции 7. Найти минимум функции
F = 4x1 - 3x2 при ограничениях F = 2x1 - x2 при ограничениях
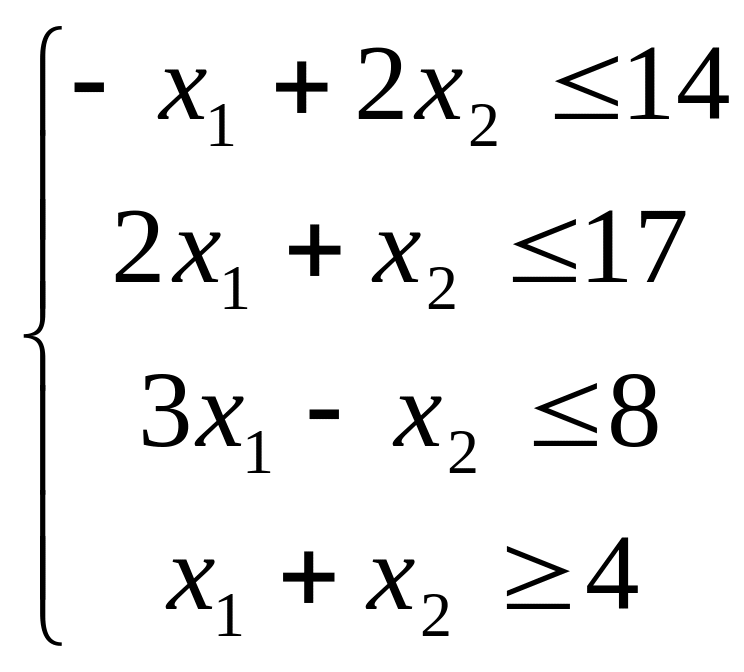

x1≥0, x2≥0.
4. Подведение итогов занятия.
5. Постановка домашнего задания.
