Практические занятия Занятие №1. Метод Жордана-Гаусса решения систем линейных уравнений План занятия:
1. Организационный момент.
2. Объяснение нового материала:
1.Система линейных уравнений. Решение системы линейных уравнений. Совместная и несовместная системы уравнений. Определенная и неопределенная системы уравнений. Запись системы уравнений в табличной форме.
2.Эквивалентные системы уравнений. Элементарные преобразования систем линейных уравнений. Теорема об элементарных преобразованиях.
3.Основная переменная. Симплексное преобразование системы линейных уравнений. Полная система основных переменных. Теорема о полной системе основных переменных. Ранг системы уравнений.
4.Алгоритм нахождения полной системы основных переменных.
5.Частное решение системы линейных уравнений. Базисное решение системы линейных уравнений. Опорное решение системы линейных уравнений. Алгоритм нахождения опорного решения.
3.Усвоение и закрепление нового материала.
Решение практических заданий
№1. Решить систему уравнений
Решение
Запишем систему уравнений в виде таблицы и, применяя симплексные преобразования относительно выделенных элементов, получим:
№ |
x1 x2 x3 x4 |
b |
1 |
1 1 -3 2 1 -2 0 -1 0 1 1 3 2 -3 2 0 |
6 -6 16 6 |
2 |
1 -1 -3 2 0 -3 3 -3 0 1 1 3 0 -5 8 -4 |
6 -12 16 -6 |
3 |
1 1 -3 2 0 1 -1 1 0 1 1 3 0 -5 8 -4 |
6 4 16 -6 |
4 |
1 0 -2 1 0 1 -1 1 0 0 2 2 0 0 3 1 |
4 4 12 14 |
5 |
1 0 -2 1 0 1 -1 1 0 0 1 1 0 0 3 1 |
6 4 16 14 |
6 |
1 0 0 3 0 1 0 2 0 0 1 1 0 0 0 -2 |
14 10 6 -4 |
7 |
1 0 0 3 0 1 0 2 0 0 1 1 0 0 0 1 |
14 10 6 2 |
8 |
1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 |
8 6 4 2 |
Отсюда следует, что исходная система уравнений имеет единственное решение
(8, 6, 4, 2).
№2. Решить систему уравнений
Решение
Запишем систему уравнений в виде таблицы и, применяя симплексные преобразования относительно выделенных элементов, получим:
№ |
x1 x2 x3 x4 |
b |
1 |
1 1 -2 1 1 -3 1 1 4 -1 -1 -1 4 3 -4 -1 |
1 0 1 2 |
2 |
1 1 -2 1 0 -4 3 0 0 -5 7 -5 0 -1 4 -5 |
1 -1 -3 -2 |
3 |
1 1 -2 1 0 -4 3 0 0 -5 7 -5 0 1 -4 5 |
1 -1 -3 2 |
4 |
1 0 2 -4 0 0 -13 20 0 0 -13 20 0 1 -4 5 |
-1 7 7 2 |
5 |
1 0 2 -4 0 0 -13/20 1 0 1 -4 5 |
-1 7/20 2 |
6 |
1 0 -3/5 0 0 0 -13/20 1 0 1 -3/4 0 |
2/5 7/20 1/4 |
Таким образом, система уравнений является неопределенной и (2/5+3/5x3, 1/4+3/4x3, x3, 7/20+13/20 x3) есть общее решение этой системы.
№3. Решить систему уравнений
Решение
Запишем систему уравнений в виде таблицы и, применяя симплексные преобразования относительно выделенных элементов, получим:
№ |
x1 x2 x3 x4 |
b |
1 |
6 -5 7 8 3 11 2 4 3 2 3 4 1 1 1 0 |
3 6 1 0 |
2 |
0 -11 1 8 0 8 -1 4 0 -1 0 4 1 1 1 0 |
3 6 1 0 |
3 |
0 -11 1 8 0 8 -1 4 0 1 0 -4 1 1 1 0 |
3 6 -1 0 |
4 |
0 0 1 -36 0 0 -1 36 0 1 0 -4 1 0 1 4 |
-8 14 -1 1 |
5 |
0 0 1 -36 0 0 1 -36 0 1 0 -4 1 0 1 4 |
6 -14 -1 1 |
6 |
0 0 0 0 0 0 1 -36 0 1 0 -4 1 0 0 40 |
6 -14 -1 15 |
Из первой строки последней таблицы следует, что 0=6. Противоречие. Значит, система уравнений решения не имеет.
В задачах №2-№7 найти опорные решения системы линейных уравнений:
№2.
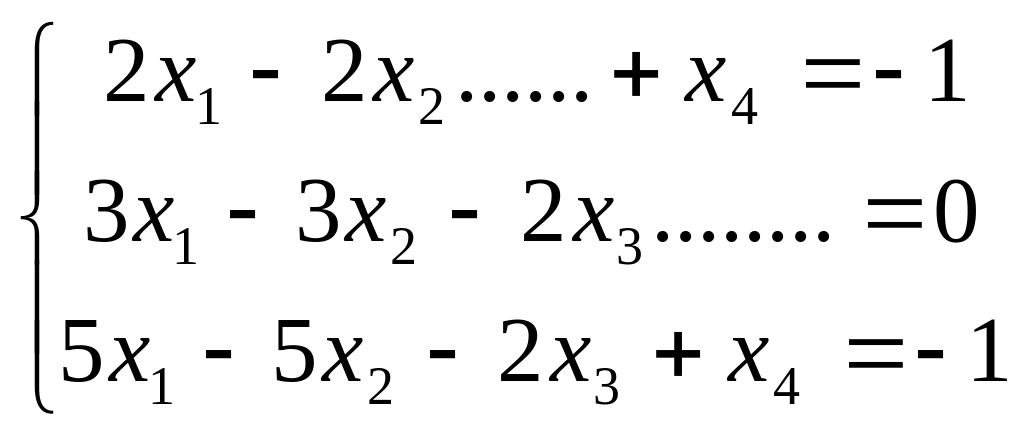№3.
№4.
№5.
№6.
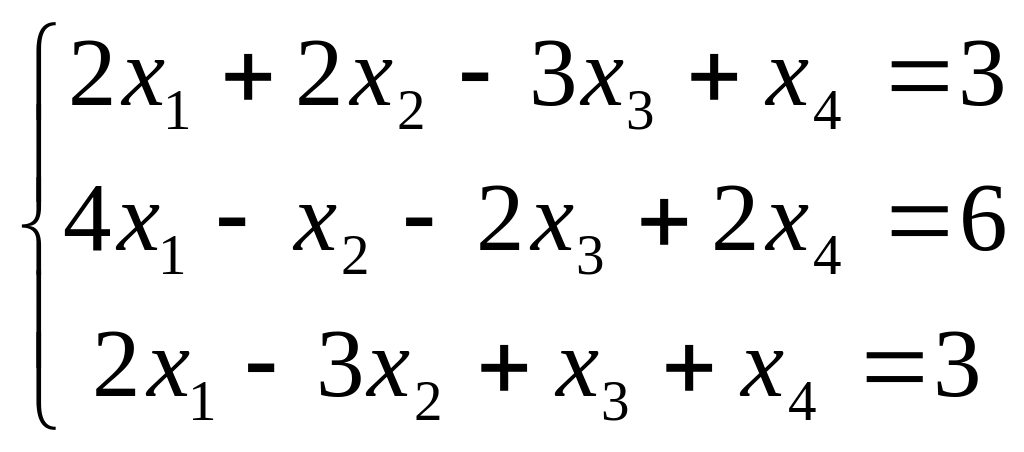№7.
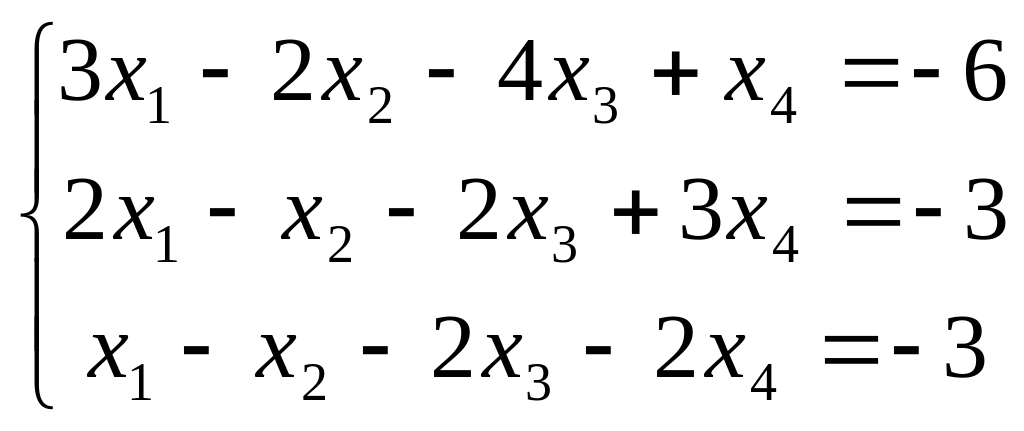
4. Подведение итогов занятия.
5. Постановка домашнего задания.