Тема: Симплексный метод решения задачи линейного программирования.

Пусть торговое предприятие реализует n групп товаров, используя при этом ограниченные материально-денежные ресурсы размером b_i 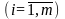. Известны расходы ресурсов i –го вида на организацию продажи единицы товарооборота товаров j-ой группы, заданные в виде технологической матрицы А = (a_ij) , ,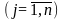 , и прибыль, получаемая предприятием от реализации единицы товарооборота товаров j-ой группы - С_j.

Требуется определить объем и структуру товарооборота Х_j , при которых общая прибыль торгового предприятия была бы максимальной.

Математическую модель задачи можно записать следующим образом:

Определить , который удовлетворяет ограничениям

, (2.1)

, (2.2)

и доставляет максимальное значение целевой функции

(2.3)

Задача линейного программирования (2.1)–(2.3) может быть решена симплексным методом, так как система ограничений задана в виде системы неравенств только смысла «≤ » и вектор столбец свободных членов содержит только положительные числа, т.е.

b_i ≥ 0.

Алгоритм симплексного метода включает следующие этапы.

1. Составление первого опорного плана.

Перейдем от системы неравенств (2.1) к системе уравнений путем введения неотрицательных дополнительных переменных. Векторы-столбцы при этих переменных представляют собой единичные векторы и образуют базис, а соответствующие им переменные называются базисными.

, (2.4)

Разрешим систему уравнений (2.4) относительно базисных переменных:

, (2.5)

Аналогично функцию цели представим в виде:

(2.6)

Полагая, что основные переменные 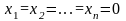, получим первый опорный план , .

Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения первого опорного плана, занести в симплексную таблицу. Первые m строк симплексной таблицы содержат коэффициенты системы ограничений и свободные члены. Последняя (m +1)-ая строка таблицы называется индексной. Она заполняется коэффициентами функции цели, взятыми с противоположным знаком.

2. Проверка оптимальности опорного плана.

Если все коэффициенты индексной строки симплексной таблицы (при решении задачи на максимум целевой функции) неотрицательны (∆ ≥ 0, , то опорный план задачи является оптимальным. Если найдется хотя бы один коэффициент индексной строки меньше нуля, план не оптимальный и можно перейти к новому опорному плану, при котором значение целевой функции увеличится. Переход к другому плану осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора.

3. Определение направляющих (разрешающих) столбца и строки.

Из отрицательных коэффициентов индексной строки ∆_j < 0 выбираем максимальный по абсолютной величине. Направляющий столбец, соответствующий выбранному коэффициенту, показывает, какой вектор или переменная на следующей итерации прейдет из свободных в базисные. Пусть, например, ∆_k < 0 и решено ввести в базис вектор А _k.

Для определения вектора (переменной), подлежащего исключению из базиса, элементы столбца свободных членов симплексной таблицы (значения базисных переменных) делим на соответствующие положительные элементы направляющего столбца для всех . Результаты заносим в столбец Θ симплексной таблицы. Строка симплексной таблицы, соответствующая минимальному значению Θ, является направляющей. Пусть этот минимум достигается при i = r. Тогда из базиса исключают вектор А_r , т.е. переменная x_r на следующей итерации выйдет из состава базисных переменных и станет свободной. Элемент симплексной таблицы а_rk , находящийся на пересечении направляющих столбца и строки, называется разрешающим.