7. Энергия деформации при изгибе и кручении стержня

В случаях сложного деформирования напряжения в твердом теле вычисляют, исходя из вариационных принципов. Для применения этих принципов надо уметь находить изменение энергии тела при деформации. Мы кратко ознакомимся с методами вычисления этой энергии в случаях простой деформации стержня.

Энергия деформируемого тела.

Обозначим:

Тогда

При этих обозначениях компоненты тензора деформаций:

тензора напряжений

Первое начало термодинамики (см. [5]) имеет вид:

где – изменение внутренней энергии, – полученное телом количество теплоты, – совершенная телом работа. В механике важна не , а свободная энергия [5]:

– температура, – энтропия. При постоянной температуре и .

При деформировании тела совершается работа [9]:

Тогда из первого начала термодинамики

Здесь принято обычное правило суммирования по повторяющимся индексам. Можно показать, что свободная энергия деформированного тела в единице объема равна

(15)

Эта же формула в старых обозначениях [9]:

(15’)

Энергия стержня при кручении.

При кручении выполняются соотношения:

По закону Гука

Подставляя эти значения в (15’), получим для свободной энергии бесконечно малого объема :

Энергия кручения отрезка стержня получается интегрированием этой формулы по площади поперечного сечения :

С другой стороны, угол поворота связан с крутящим моментом формулой:

откуда следует

Заменяя обратно , получим энергию единицы длины стержня при кручении:

Полную свободную энергию стержня длины при кручении получим интегрированием:

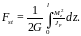(16)

Энергия стержня при изгибе.

При чистом изгибе стержня выполнены соотношения:

Отсюда свободная энергия единицы объема:

Ранее для кривизны изогнутого стержня найдено:

Интегрируя по площади поперечного сечения, найдем энергию единицы длины стержня:

Подставим выражение для кривизны:

Полную энергию изогнутого стержня найдем интегрированием:

Выразим моменты и энергию через прогибы стержня :

8. Принцип виртуальной работы

Формулировка принципа виртуальной работы. Если тело находится в состоянии равновесия, то полная работа всех сил, действующих на него, на любом виртуальном перемещении равна нулю.

Определение. Виртуальное перемещение — любое малое перемещение, совместимое с условиями сплошности материала и условиями закрепления.

Виртуальные перемещения еще называются вариациями перемещений и обозначаются , , . Математически принцип виртуальной работы записывается так:

Здесь – сумма проекций на ось всех сил, внешних и внутренних.

Работа внутренних сил равна изменению свободной энергии, взятому с обратным знаком:

где – вариации деформаций. Знак минус потому, что работа совершается против сил взаимодействия между частицами.

Работа внешних сил.

Внешние силы делятся на:

а) Поверхностные силы , , , действующие на элемент поверхности .

б) Объемные силы , , , действующие на элемент объема .

В состоянии равновесия полная виртуальная работа равна нулю:

Поскольку внешние силы заданы явно, то операцию варьирования можно вынести за интеграл. Считая объемные силы равными нулю, получим:

(17)