4. Введение в механику стержня. Кручение и изгиб стержня

Сделаем несколько вводных замечаний.

Определение. Стержень — твердое деформируемое тело, один из размеров которого превышает два других.

Для стержня, как и для любого объекта, выполняются уравнения (2). Условия на поверхности получим, выписав соотношения для напряжений на произвольной площадке с нормалью :

(7)

Обратим закон Гука (6), выразив напряжения через деформации

(8)

Также выполнены соотношения Коши (5).

4.1. Простейшие задачи механики стержня

Рассмотрим простые задачи, которые можно найти в [8], .

a) Растяжение в осевом направлении.

Здесь объемные силы обращаются в ноль по постановке задачи. Пусть на концы стержня действуют растягивающие силы . Уравнения (2) удовлетворены, если

На концах стержня выполняется соотношение

то есть внешние силы равномерно распределены по концевым сечениям стержня.

б) Кручение круглого вала.

На концах круглого стержня действуют противоположно направленные крутящие моменты . Для кручения закон Гука имеет вид

Для деформаций можно получить формулу

где – угол сдвига сечения, – расстояние от рассматриваемой точки до центра сечения. Обозначим – относительный угол закручивания. Тогда для напряжения получим

Разложим на компоненты

где – декартовы координаты в плоскости поперечного сечения. В элементарной теории принято

Поскольку компоненты тензора напряжений в данной задаче являются линейными функциями координат, то уравнения равновесия (2) выполнены и осталось проверить условия на поверхности. Боковая поверхность вала свободна от усилий и на ней . Отсюда и из (7) получим

(*)

Для круглого цилиндра

Подставим в (*) значения , и получим

это тождество.

Таким образом, предположения элементарной теории оправданы, если поверхностные касательные усилия на торцах стержня распределены так же, как напряжения и в промежуточных сечениях вала.

Принцип Сен-Венана (1855 г.). Распределение напряжений в стержне и пластине зависит только от величины и направления внешней нагрузки, но не от способа ее приложения.

Значит, на большом расстоянии от концов стержня распределение внутренних напряжений зависит только от величины крутящего момента.

в) Чистый изгиб стержня.

Пусть стержень изгибается двумя изгибающими моментами , приложенными на его концах, в плоскости . Элементарная теория дает

– радиус кривизны стержня после изгиба. Граничные условия на боковых поверхностях удовлетворены тождественно. На концах поверхностные силы распределены как .

Найдем отсюда изгибающий момент. По определению он равен

Здесь – момент инерции поперечного сечения. Методом сечений можно найти . Для радиуса кривизны получим

Перемещения можно найти из соотношений Коши (5). При этом предположим, что точка закреплена и . Тогда при , , :

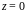Закон Гука дает:

На оси стержня , получим

Последняя формула выражает перемещения вдоль оси , а следовательно, прогибы стержня при чистом изгибе.

4.2. Теорема Журавского-Шведлера

Выделим двумя поперечными сечениями элемент стержня длиной , находящийся под внешней распределенной нагрузкой (рис. 6).

Рис. 6. К доказательству теоремы Журавского-Шведлера

На рис. 6 на элемент действуют внутренние силовые факторы:

– изгибающие моменты от отсеченных левой и правой частей;

– поперечные усилия.

Составим уравнения равновесия элемента :

Из этих уравнений, отбрасывая вторые порядки малости, найдем:

Следующие формулы выражают математически теорему Журавского-Шведлера:

(9)

где , – значения поперечной силы и изгибающего момента при .