13. Равновесие прямоугольной пластины

Рис. 15. Геометрия задачи и краевые условия

Рассмотрим шарнирно опертую по краю пластинку. Для нее краевая задача имеет вид:

при (26)

при

Решение ищем в виде двойного тригонометрического ряда:

В математической теории упругости применяют сокращенную запись:

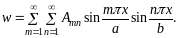(27)

Задача сводиться к определению коэффициентов Ряд (27) удовлетворяет краевым условиям в силу того, что .

Для определения надо разложить нагрузку q(x,y) в ряд, аналогичный (27), найти производные от w, подставить все эти данные в уравнение (26) и сравнить эти коэффициенты при одинаковых тригонометрических функциях слева и справа. Сделаем это:

где известно из курса математического анализа.

Собирая все результаты, получим:

(28)

Сравнивая левую и правую части, получим:

, откуда

Таким образом, функция (27) полностью определена. Частные случаи:

1) Нагрузка равномерно распределена по поверхности, q=const:

при нечетных m=1,3,5..; n=1,3,5… (при четных индексах интеграл обращается в ноль).

Подставляя в решение (27), получим:

, (m, n=1,3,5,..) (29)

Изгибающие моменты выражаются через прогибы по формулам:

Вторые производные равны:

.

Подставляя эти выражения в формулы для моментов, получим:

Максимальные изгибающие моменты возникают в центре пластины при . Для составления таблиц их представляют в виде:

, где - функции отношения . Ряд (30) сходится медленнее, чем (29), так как степень числителя выше.

Эпюры изгибающих моментов получаются табулированием функций (30). Для их построения надо оставить 4 слагаемых в ряде, т.е. члены для значений m = 1;3, n=1;3 и табулировать (30) с шагом по x, по y. Ошибка при этом не превышает 3% от точного значения.

2) Сила Р сосредоточена в точке К с координатами , . Тогда, используя - функцию, получим:

Тогда для прогибов получим:

Этот ряд сходиться медленно, ряды же для и сходятся еще медленнее. Поэтому эту методику можно использовать в данном случае только для нахождения прогибов. После определения можно на компьютере численно найти и построить эпюры изгибающих моментов.

14. Применение вариационных принципов к расчету пластин

14.1. Энергия тонкой пластинки

При , формула для удельной энергии деформации принимает вид [6]:

. (31)

Вспоминая формулы для напряжений и деформаций

;

.

получим

(32)

Энергия всей пластинки:

.

Потенциальная энергия растянутого стержня:

. (33)

14.2. Вариационные принципы при расчете пластин

При исследовании задач теории упругости часто используют вариационные методы. Варьирование функции – операция, похожая на дифференцирование. Подробно об этой операции можно узнать из [5]. Вариационные методы часто называют энергетическими, потому что они основаны на понятиях работы сил и энергии деформации.

Принцип возможных перемещений: разность между работой внешних сил и полной энергией деформации твердого тела минимальна только на действительном перемещении этого тела.

Математически это означает, что деформация тела, имеющая место в действительности, минимизирует разность:

(34)

При изгибе пластинки работа внешних сил равна:

, – внешняя нагрузка, – прогиб пластинки. Потенциальная энергия получается после интегрирования по всей площади пластинки:

Если выбрать вид функции прогиба:

где – известные функции, удовлетворяющие граничным условиям, то условие минимальности примет вид:

(35)

После этих выкладок становится ясен алгоритм решения задачи о равновесии пластинки (метод Ритца):

1. Задаем базисные функции .

2. Находим выражения для .

3. Из условия (35) получим уравнений для неизвестных коэффициентов . Это будут линейные алгебраические уравнения.

4. Найдем и подставим в выражения для прогиба пластины , решив тем самым задачу.

Подробно этот метод изложен в учебнике [8].

Пример расчета пластинки с использованием принципа минимума энергии деформации.

Рассматривается задача о растяжении в своей плоскости прямоугольной пластинки напряжениями, приложенными вдоль ее краев по параболическому закону (рис. 16).

Пластинка растянута усилиями:

при (парабола);

при

Нагрузка вдоль оси, перпендикулярной плоскости пластины, равна нулю, поэтому . В учебнике [10] утверждается, что энергия деформации пластинки единичной толщины в этом случае равна:

(36)

Рис. 16. Нагружение пластины в ее плоскости

Так как распределение напряжений в прямоугольной пластине не зависит от упругих констант материала, положим в (36) Введем функцию напряжений следующим способом:

Тогда энергия пластинки выразится через функцию напряжений:

Функцию напряжений будем искать в виде:

.

При этом все должны удовлетворять краевым условиям, а коэффициенты находим из условий

… .

Пусть при этом краевые условия выполнены. Тогда получим уравнение для неизвестной

Для квадратной пластинки со стороной :

Зная , можно определить неизвестные напряжения. Фактически при решении этой задачи использован метод Ритца.