9.2. Пределы применимости формулы Эйлера

Критическое напряжение, по определению, равно

Формула Эйлера применима, если выполнен закон Гука, то есть

где – предельно допустимое напряжение на сжатие. По Эйлеру:

Здесь обозначено

­ гибкость стержня.

Отсюда условие применимости формулы Эйлера запишется в виде:

Определение. Величина называется предельной гибкостью стержня.

Эта величина приведена в справочниках. Если гибкость меньше предельной, то вместо расчета на устойчивость нужен расчет на прочность. Предельная гибкость – это физический параметр материала.

Пример. Проверить на устойчивость сжатую стойку трубчатого сечения из хромомолибденовой стали ( МПа, МПа), если требуемый коэффициент запаса устойчивости . Сжимающая сила кН, длина стойки м, внутренний и внешний диаметры мм, мм, коэффициент приведения длины .

Решение.

Предельная гибкость

Момент инерции сечения:

Площадь сечения

Гибкость

следовательно, применима формула Эйлера. В единицах СИ получим:

Коэффициент запаса устойчивости

Таким образом, заданные условия устойчивости стойки выполнены.

10. Расчет вала с прямым изгибом

10.1. Теории прочности

При совместном действии изгиба и кручения в вале возникает сложное напряженное состояние. В этом случае нельзя ограничиться нахождением только для расчета на прочность, надо учесть влияние и других компонент тензора напряжений. Если привести этот тензор к диагональному виду, то, согласно диаграмме Мора, получим

где -максимальное главное значение напряжения, -минимальное, -максимальное касательное напряжение. Так как наибольшее ограничение на прочность накладывается именно максимальным касательным напряжением, за критерий прочности часто принимают величину

Когда в основу кладется эта величина, говорят о третьей теории прочности. называется эквивалентным напряжением и при расчете пользуются следующим условием прочности:

При четвертой теории прочности под эквивалентным напряжением понимают такое напряжение растяжения, при котором потенциальная энергия деформации равна энергии деформации образца. Это означает, что для эквивалентного напряжения принимают формулу:

Упрощенное плоское напряженное состояние.

Выразим экстремальные главные напряжения в предположении, что напряженное состояние является плоским и от нуля отличны только , . При этом

где – изгибающий момент, – момент сопротивления.

Рис.9. Плоское напряженное состояние

Рассматривая площадку, нормаль к которой наклонена к оси , совпадающей с продольной осью стержня, под углом (рис. 9), для нормального и касательного напряжения на ней из условий равновесия призмы получим:

Из условия экстремальности напряжения найдем , с другой стороны, условие равенства нулю касательных напряжений дает:

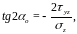
то есть экстремальные нормальные напряжения возникают на тех площадках, на которых касательные равны нулю.

Подставляя в формулу для , получим:

При этом , то есть эти напряжения главные, и :

Отсюда максимальное касательное напряжение

По гипотезам прочности:

При практическом расчете валов рекомендуется пользоваться третьей теорией прочности.