Занятие № 1. Выборочный метод. Оценка параметров генеральной совокупности

АЛГОРИТМ ОБРАБОТКИ РЕЗУЛЬТАТОВ ПРИ ВЫБОРОЧНЫХ ИССЛЕДОВАНИЯХ

I. Пусть в результате выборочного исследования количественных признаков была получена выборка малого объема n<30: Х { х₁, х_{2, …,} х_n}

1. Проводим описание выборки, т.е. ранжируем ее и результат представляем в виде ряда распределения при помощи таблицы и графика (полигона частот).

Ранжированные значения вариант
Частота повторения варианты в выборке

2. Вычисляем выборочные характеристики центра распределения:

1. Выборочная средняя .

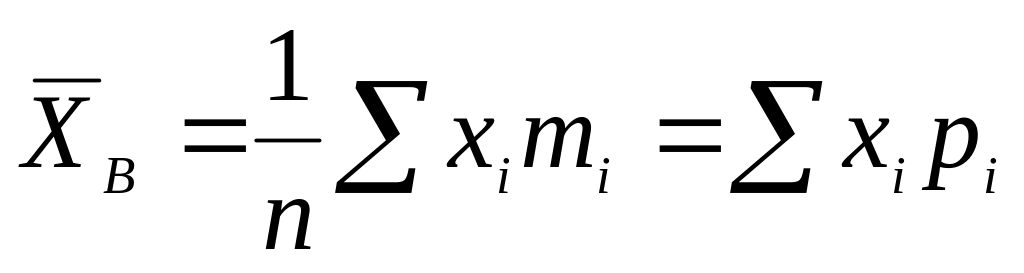2. Мода М₀ – варианта, имеющая наибольшую частоту в распределении.

3. Медиана М_е – значение, делящее число вариант пополам.

3. Вычисляем выборочные характеристики вариации:

1. Размах колебаний (размах вариации) выборки

2. Линейное отклонение вариант от выборочного среднего

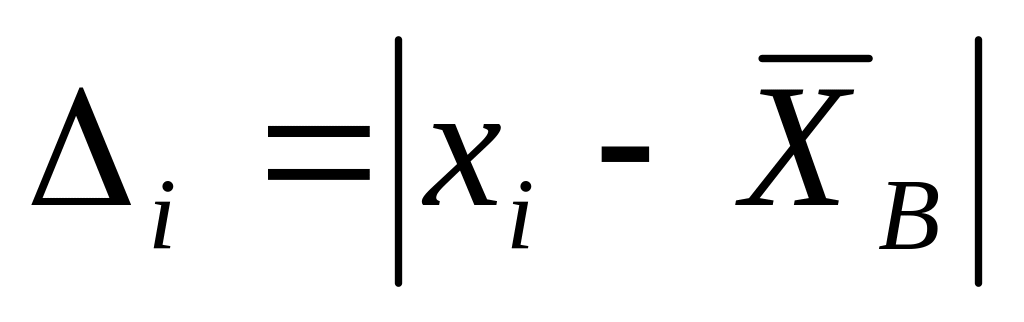
3. Среднее линейное отклонение

4. Выборочная дисперсия

5. Выборочное среднее квадратическое отклонение

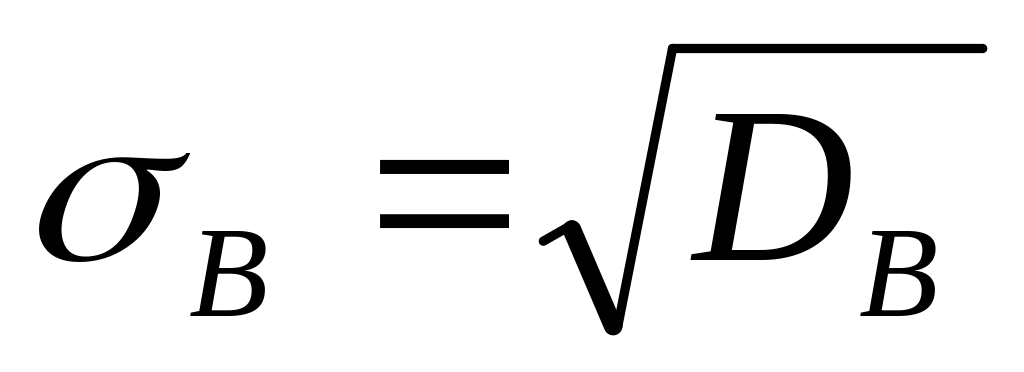
6. Коэффициент вариации

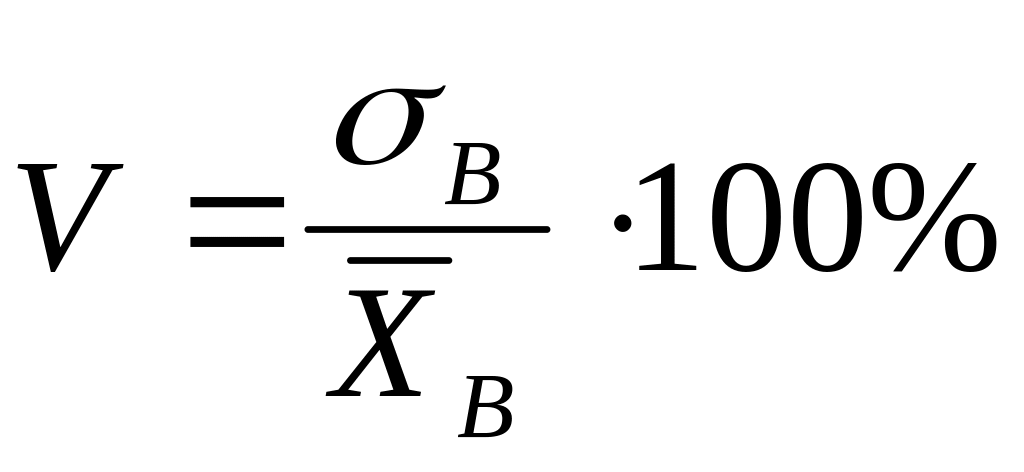
II. Пусть в результате выборочного исследования количественных признаков была получена выборка большого объема n>30: Х { х₁, х_{2, …,} х_n}

1. Разбиваем выборку на k малых интервалов в зависимости от её объема

Объем выборки n	25-40	40-60	60-100	100-200	>200
Количество интервалов разбиения k	5-6	6-8	7-10	8-12	10-15

2. Строим ранжированную таблицу распределения

Интервал разбиения	[xi; xi-1)
Середина интервала
Частота в интервале	mi
Кумулятивная (накопленная) частота к концу интервала	si

3. Строим графики (гистограмму частот и кумуляту) в осях (х; р) и (x; s) соответственно.

4. Вычисляем выборочные характеристики центра распределения:

1. Выборочная средняя

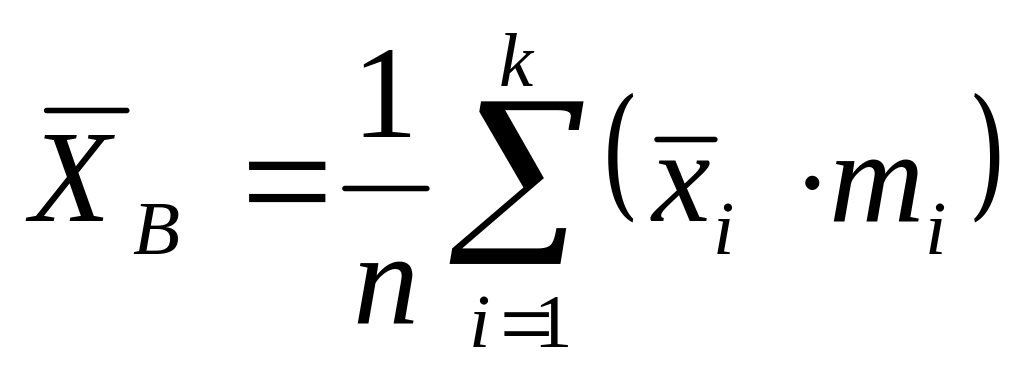
2. Мода – варианта, имеющая наибольшую частоту в распределении

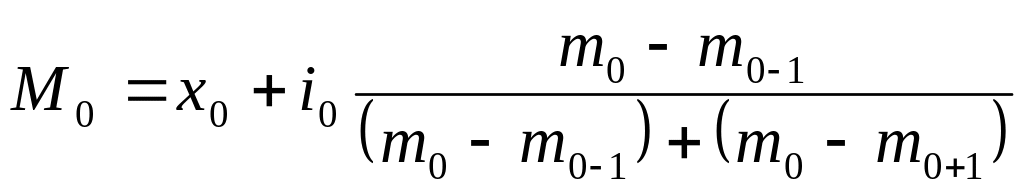
3. Медиана – значение, делящее число вариант пополам

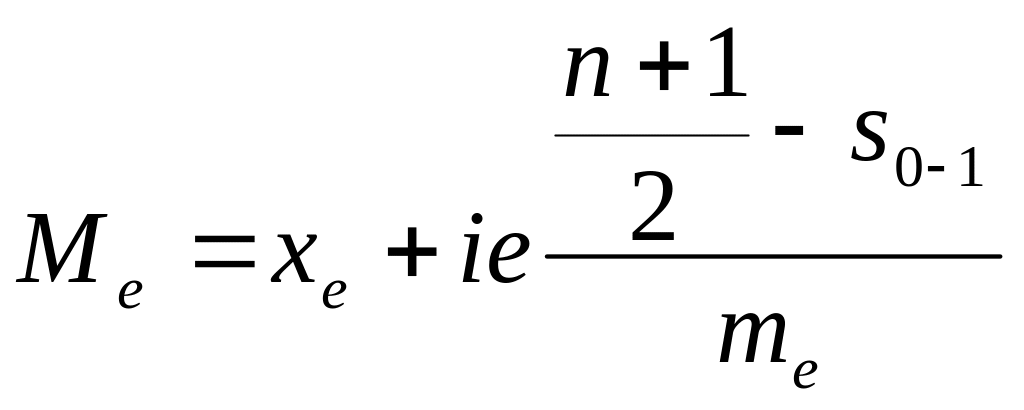
5. Вычисляем выборочные характеристики вариации:

1. Размах колебаний (размах вариации) выборки

2. Линейное отклонение вариант от выборочного среднего

3. Среднее линейное отклонение

4. Выборочная дисперсия

5. Выборочное среднее квадратическое отклонение

6. Квартильное отклонение

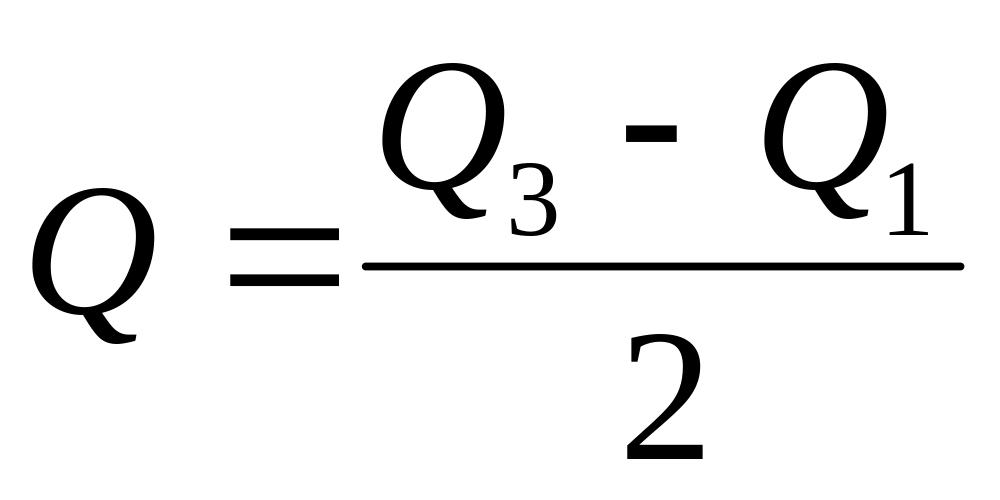
Квартили – значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% вариант будут меньше первого квартиля по величине, 25% вариант будут заключены между первым и вторым квартилями, 25% - между вторым и третьим , и остальные 25% превышают , т.е. это значения делящие число вариант на четыре части:

; ;

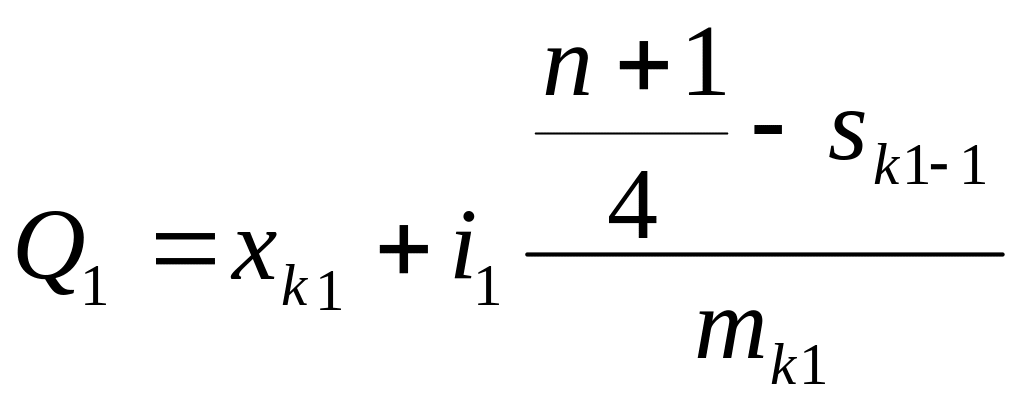7. Коэффициент децильной дифференциации

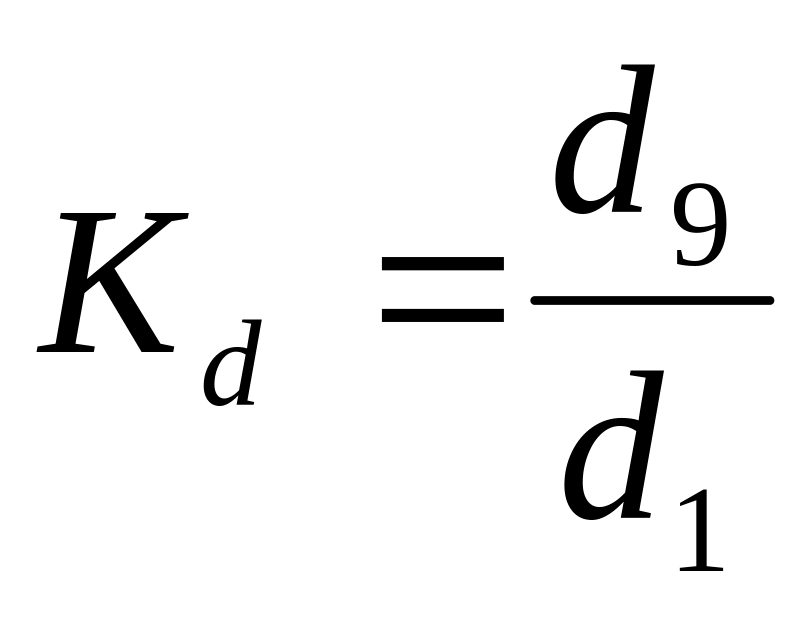
Децили – значения, делящие число вариант на десять равных частей:

;
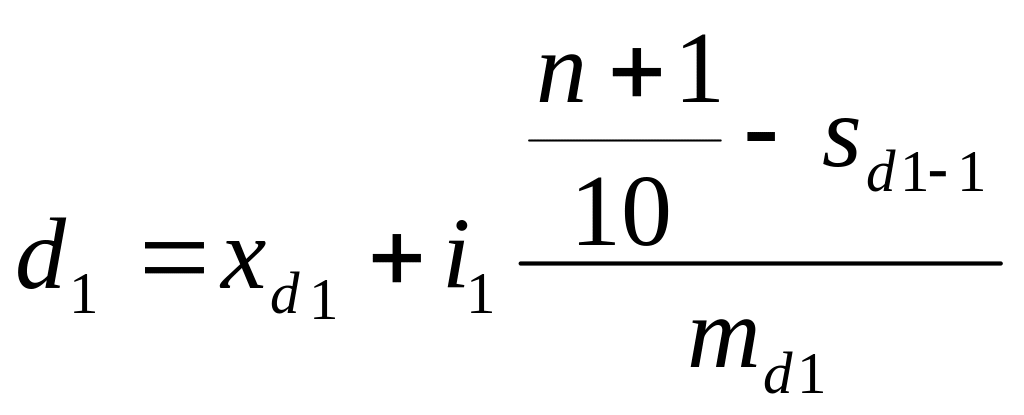