Лекция №2. Законы Кирхгофа. Расчёт эл. Цепей постоянного тока

Первый закон Кирхгофа.

Алгебраическая сумма токов в любом узле любой электрической цепи равна нулю:

.

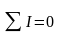Рис. 2.1

или сумма токов, направленных к узлу, равна сумме токов, направленных от него (рис. 2.1).

I₁+I₂+ I₅ = I₃+ I₄.

Правило: если ток направлен в узел, то перед ним в уравнении ставится «+», если ток направлен от узла, то «−» .

Второй закон Кирхгофа.

Алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС внутри этого контура (рис. 2.2).

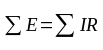(2.1).

Рис. 2.2

При составлении системы уравнений для расчёта токов эл.цепей необходимо пользоваться определёнными правилами.

Правило. Если направление тока I_i и Е совпадает с направлением обхода контура, то в уравнении эти символы записываются со знаком «+», если не совпадает, то со знаком «−».

E₁-E₂+E₃ = I₁R₁+ I₂R₂+ I₃R₃+ I₄R₄

Для проверки правильности проведенных расчётов можно использовать уравнение энергетического баланса, т. е. алгебраическая сумма мощностей, отдаваемых источниками энергии, равна сумме мощностей, поглощаемых приёмниками

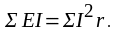
Универсальным методом анализа и расчёта сложных цепей, т.е. разветвлённых цепей с несколькими источниками питания является метод непосредственного применения первого и второго законов Кирхгофа соответственно для узловых точек и замкнутых контуров.

Непосредственное применение законов Кирхгофа для расчёта цепей основано на составлении связанных между собой уравнений. Эти уравнения могут быть получены, если известны величины э.д.с. и их направления.

Применяя законы Кирхгофа, можно составить столько уравнений, сколько неизвестных токов имеется в этой цепи. Однако для составления этих уравнений необходимо предварительно задаться произвольными направлениями неизвестных токов, которые принято считать положительными.

Если в результате решений системы уравнений величина тока имеет знак «+», это означает, что его направление совпадает с ранее выбранным направлением. В противном случае фактическое направление противоположно выбранному направлению.

Для составления требуемого числа независимых уравнений следует применить первый закон Кирхгофа ко всем узловым точкам, кроме одной, т.е. составить (q-1) уравнений, где q- число узлов схемы.

Недостающие уравнения должны быть составлены по второму закону Кирхгофа так, чтобы каждое следующее уравнение не могло быть получено из предыдущих уравнений. В схеме (см. рис.2.2) имеем 4 узла, а число замкнутых контуров -1, а во всяком замкнутом контуре алгебраическая сумма э.д.с. равна алгебраической сумме падений напряжений на всех сопротивлениях, входящих в этот контур.

Таким образом, для расчёта токов в цепях (см. рис.2.2) необходимо составить 4 уравнения, т.е.

Расчёт эл. Цепей постоянного тока, методы расчёта

Простые цепи. Простая цепь – цепь, содержит один источник энергии (рис.2.3) При расчёте эл.цепей необходимо определять эквивалентные сопротивления

Последовательное соединение сопротивлений

U

Рис. 2.3

Второй закон Кирхгофа для этой схемы будет иметь вид

U = U₁ + U₂ + U₃ .

Поделим это уравнение почленно на ток I : U/I = U₁ /I + U₂ /I + U₃ /I, получим

R = R₁+ R₂+ R₃.

Таким образом, при последовательном соединении сопротивлений эквивалентное сопротивление равно сумме последовательно соединенных R.

Цепи с параллельным соединением сопротивлений (рис. 2 4).

Рис. 2.4

Для преобразования этой схемы используется первый закон Кирхгофа и закон Ома.

I₁ = U/R₁ , I₂ = U/R₂ , I₃ = U/R₃ , I = I₁+ I₂ + I₃ ,

U/R_Э = U/R₁+U/R₂+U/R₃.

Тогда эквивалентная проводимость

1/R_Э = 1/R₁+1/R₂+1/R₃ , G_Э = G₁+G₂+G₃.

Таким образом, при параллельном соединении сопротивлений эквивалентная проводимость равна сумме проводимостей, а выражение для эквивалентного сопротивления примет вид

R_Э = .

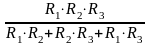Используя эту формулу и умножив по закону Ома на U, получим баланс мощности эл.цепи, т.е.

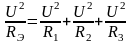или

Р=Р₁+Р₂+Р_3.

Цепи со смешанным соединением сопротивлений

На рис. 2.5 представлена схема простой цепи, но со смешанным соединением сопротивлений и эквивалентная схема её замещения

Р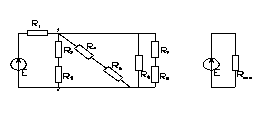 ис. 2.5- Схема простой цепи и эквивалентная схема замещения её.

Практически все простые цепи рассчитываются при помощи метода свёртывания и развёртывания.

R₆₇₈=R₆(R₇+R₈)/(R₆+R₇+R₈),

R_4-8= R₆₇₈(R₄+R₅)/(R₄+R₅+R₈₇₆),

R₂₈= R_4-8(R₂+R₃)/(R₂+R₃+R_4-8),

R_экв=R₁+R_2,8

I₁=E/(R₁+R₂₈),

U₁₂=I₁R₂₈

I₂=U₁₂/(R₂+R₃),

I₃=U₁₂/(R₄+R₅),

I₅=U₁₂/(R₇+R₈),

I₄=U₁₂/R_6.