2. Критериальный язык описания выбора

На примере описания выбора видно, как об одном и том же явлении можно говорить на языках различной общности. К настоящему моменту сложилось три основных языка описания выбора. Самым простым, наиболее развитым и чаще употребляемым в приложениях является критериальный язык. Это название связано с основным предположением, состоящим в том, что каждую отдельно взятую альтернативу можно оценить конкретным числом (значением критерия), и сравнение альтернатив сводится к сравнению соответствующих им чисел.

Основой критериального языка описания выбора является предположение о возможности оценить каждую отдельно взятую альтернативу определенным числом. При этом выбор сводится к отысканию альтернативы с наибольшим значением критериальной функции.

П усть x – некоторая альтернатива из множества X. Считается, что для всех x  X может быть задана функция q(x), которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности и т. д.) и обладает тем свойством, что если альтернатива x₁ предпочтительнее альтернативы x₂ (будем обозначать это x₁ > x₂), то q(x₁) > q(x₂) и обратно.

Многокритериальные задачи не имеют однозначного общего решения. Поэтому предлагается много разных способов придать многокритериальной задаче частный вид, обладающий единственным решением. Естественно, что для разных способов эти решения в общем случае оказываются различными. Поэтому едва ли не главное в решении многокритериальной задачи – обоснование именно данного вида ее постановки.

Выбор как максимизация критерия

Если теперь сделать еще одно важное предположение, что выбор любой альтернативы приводит к однозначно известным последствиям (т.е. считать, что выбор осуществляется в условиях определенности) и заданный критерий q(x) численно выражает оценку этих последствий, то наилучшей альтернативой x* является, естественно, та, которая обладает наибольшим значением критерия:

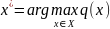(1)

Задача отыскания x*, простая по постановке, часто оказывается сложной для решения, поскольку метод ее решения (да и сама возможность решения) определяется как характером множества X (размерностью вектора x и типом множества X – является ли оно конечным, счетным или континуальным), так и характером критерия (является ли q(x) функцией или функционалом и какой или каким именно).

Однако сложность отыскания наилучшей альтернативы существенно возрастает, так как на практике оценивание любого варианта единственным числом обычно оказывается неприемлемым упрощением. Более полное рассмотрение альтернатив приводит к необходимости оценивать их не по одному, а по нескольким критериям, качественно различающимся между собой.

Например, при выборе конструкции самолета проектировщикам следует учитывать множество критериев: технических (высотность, скорость, маневренность, грузоподъемность, длительность полета и т.д.), технологических (связанных с будущим процессом серийного изготовления самолетов), экономических (определяющих затраты на производство, эксплуатацию и обслуживание машин, их конкурентоспособность), социальных (в частности, уровень шума, загрязнение атмосферы), эргономических (условия работы экипажа, уровень комфорта для пассажиров) и пр.

Итак, пусть для оценивания альтернатив используется несколько критериев q_i(x), i = 1, ..., p. Теоретически можно представить себе случай, когда во множестве X окажется одна альтернатива, обладающая наибольшими значениями всех p критериев; она и является наилучшей. Однако на практике такие случаи почти не встречаются, и возникает вопрос, как же тогда осуществлять выбор (так, например, на рис. 1 множеству X соответствуют точки на плоскости значений двух критериев q₁ и q₂; оба критерия желательно максимизировать).

1. 

   Рис.1. Иллюстрация методов решения многокритериальных задач: а) оптимизация по одному “суперкритерию”, являющемуся линейной комбинацией частных критериев; 6) метод уступок; в) задание уровней притязания; г) нахождение паретовского множества альтернатив

   Сведение многокритериальной задачи к однокритериальной

Рассмотрим наиболее употребительные способы решения многокритериальных задач. П ервый способ состоит в том, чтобы многокритериальную задачу свести к однокритериальной. Это означает введение суперкритерия, т.е. скалярной функции векторного аргумента:

q₀(x) = q₀(q₁(x), q₂(x), ..., q_p(x)). (2)

Суперкритерий позволяет упорядочить альтернативы по величине q₀, выделив тем самым наилучшую (в смысле этого критерия). Вид функции q₀ определяется тем, как мы представляем себе вклад каждого критерия в суперкритерий; обычно используют аддитивные или мультипликативные функции:

; (3)

. (4)

Коэффициенты s_i обеспечивают, во-первых, безразмерность числа q_i/s_i (частные критерии могут иметь разную размерность, и тогда некоторые арифметические операции над ними, например сложение, не имеют смысла) и, во-вторых, в необходимых случаях (как в формуле (4)) выполнение условия β_iq_i/s_i  1. Коэффициенты α_i и β_i отражают относительный вклад частных критериев в суперкритерий.

Итак, при данном способе задача сводится к максимизации суперкритерия:

(5)

Очевидные достоинства объединения нескольких критериев в один суперкритерий сопровождаются рядом трудностей и недостатков, которые необходимо учитывать при использовании этого метода. Оставив в стороне трудности построения самой функции и вычислительные трудности ее максимизации, обратим внимание на следующий очень важный момент. Упорядочение точек в многомерном пространстве в принципе не может быть однозначным и полностью определяется видом упорядочивающей функции.

С уперкритерий играет роль этой упорядочивающей функции, и его даже “небольшое” изменение может привести к тому, что оптимальная в новом смысле альтернатива окажется очень сильно отличающейся от старой. На рис. 1, а видно, как изменяется выбор наилучшей альтернативы при простой смене коэффициентов в линейной упорядочивающей функции (3), что отражается в изменении наклона соответствующей прямой: q₀₁(x₁*) > q₀₁(x₂*), но q₀₂(x₁*) < q₀₂(x₂*). Заметим, что линейные комбинации частных критериев придают упорядочению следующий смысл: “чем дальше от нуля в заданном направлении, тем лучше”. На рис. 1, а направления, соответствующие суперкритериям q₀₁ и q₀₂, изображены стрелками. Идея такого упорядочивания в многомерном пространстве заложена в некоторых балльных системах оценки вариантов.

Другой вариант поиска альтернативы, самой удаленной от нуля в заданном направлении, дает максимизация минимального критерия [23]:

(6)

что означает поиск вокруг направления α_iq_i/s_i = const методом “подтягивания самого отстающего”.