6. Выбор на нечетком множестве альтернатив

Л юбая задача выбора является задачей целевого сужения множества альтернатив. Как описание альтернатив (перечень их признаков, параметров и т.п.), так и описание правил их сравнения (критериев, отношений) даются в терминах той или иной измерительной шкалы (см. § 6.2). Известно, что любая измерительная шкала допускает неточность (см. § 6.3). Точнее говоря, в жизни мы часто сталкиваемся с ситуациями, описать которые можно лишь в интервалах шкалы. Это, разумеется, относится и к ситуациям, приводящим к выбору. В результате мы приходим к задачам выбора в условиях интервальной неопределенности. Каждой из задач, рассмотренных в предыдущих параграфах, можно поставить в соответствие несколько интервальных задач, поскольку неточными могут оказаться все или только некоторые компоненты задачи. До настоящего времени рассмотрено лишь незначительное число таких задач, однако ведется работа в этом направлении.

Правила выбора в нечеткой ситуации, естественно, являются различными в зависимости от того, что именно нечетко в этой ситуации. Задача выбора решается просто и изящно, если критериальные функции отождествляются с функциями принадлежности. Однако на практике встречаются и другие задачи; например, интервальным может быть любой параметр критериальной функции, которая сама не является функцией принадлежности.

Многокритериальный выбор в нечеткой ситуации

У же в первой работе по принятию решений в интервальной ситуации Беллман и Задэ [4] выдвинули идею, состоящую в том, чтобы и цели, и ограничения представлять как нечеткие множества на множестве альтернатив (в случае одной цели и одного ограничения это соответствует заданию множеств G = {x, μ_G(x)} и C = {x, μ_C(x)}). Следующий важный шаг состоял в определении размытого решения D как пересечения размытой цели G и размытого ограничения C, т.е. (см. § 6.3)

μ_D(x) = min [μ_G(x), μ_C(x)]. (1)

Обобщение на случай большего числа условий очевидно. Если из размытого множества D требуется выделить какую-то одну альтернативу, то можно поступать по-разному (вплоть до рандомизации выбора), но возможный вариант состоит в максимизации μ_D(x):

. (2)

При таком изложении задачи выбора напрашивается идея о том, чтобы вообще функцию принадлежности i-му условию интерпретировать как i-й критерий качества и вернуться к многокритериальным задачам. Тогда соотношение (1) оказывается формой суперкритерия (1) § 7.2, которая далеко не единственна.

Интересны исследования в этом направлении, сделанные Эстером [45]. Он рассмотрел суперкритерий вида

, (3)

где 0  g_i  1, 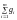 = 1; m – число размытых условий; μ_i(x) – функция принадлежности i-му условию; p – параметр суперкритерия. Представление (3) интересно не только наличием свойств, облегчающих математическое рассмотрение задачи (например, монотонность и непрерывность по всем компонентам), но и тем, что оно охватывает широкий класс частных суперкритериев. Так, при p  –  получается оператор нахождения минимального элемента из заданной совокупности (т.е. снова приходим к формуле (1)), при p = 0 – оператор умножения, при p = 1 – оператор сложения, при p  +  – оператор нахождения максимального элемента. Итак, задача нахождения наилучшей альтернативы x* сводится к максимизации Z^p(x):

. (4)

Очевидно, что при этом решение зависит от конкретного набора коэффициентов g = {g_i}. Обозначим через E(p) множество {x^g*}, соответствующее разным g при фиксированном p. Эстер обнаружил [46] интересные свойства множеств E(p): для всех –  < p₁  p₂ <  справедливо включение E(p₂)  E(p₁)  РМ, где РМ – паретовское множество (см. § 7.2).

Функции принадлежности вообще находить непросто (см. § 6.3), а при использовании изложенного подхода, кроме того, требуется, чтобы они еще имели и смысл критериальных функций в задаче выбора. Это может оказаться и неудобным, и бессмысленным.

Заканчивая обзор нечетких критериальных задач выбора, рассмотрим еще задачи, связанные с использованием расстояний между точками в пространстве альтернатив. При расплывчатом описании альтернатив предлагается “расстояние” определять через модули разностей функций принадлежности, например

, (5)

где μ_r(x) – функция принадлежности по r-му признаку к интересующему нас множеству. Такие расстояния используются в задачах классификации [17].