2.2 2 Тапсырманың орындалуы

2.2.1 Импульстің математикалық моделі

Берілген ипмульс мына формуламен өрнектеледі:

мұндағы – Хэвисайд функциясы деп аталады.

2.2.2 Импульстің спектрлік тығыздығы

Импульстің спектрлік тығыздығын анықтау үшін Фурьенің тура түлендіруін қолданамыз

Амплитудалық спектр:

Фазалық спектр:

2.2.3АЖС және ФЖС-тің спектралдық тығыздығы

2-сурет. АЖС тығыздығы

3-сурет . ФЖС тығыздығы

2.2.4 Уақыттың кідіруі мен импульс ұзақтығының АЖС және ФЖС-тің спектр тығыздығына әсер етуі

Айталық, бізге белгілі сигналының спектрлік тығыздығы болсын. Осы сигналды уақытқа кешіктірсек сигнал түрге енеді. Алынған сигналды Фурье түрлендіруіне салайық:

уақытқа кешіктірілген сигналдың спектрлік жиілігі амплитудалық мәні бойынша өзгеріссіз қалып тек фазасы бойынша 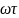бұрышқа кешігеді.

4-сурет. кешіккен сигнал АЖС тығыздығы

5-сурет. кешіккен сигнал ФЖС тығыздығы

Ұзақтығы екі есе кіші импульсті келтірейік. Айталық сигналдың әрекет ету уақыты ( ) k есе азайсын. Осы кезде спектрлік тығыздық қалай өзгеретінін есептейік:

Екі есе қысқа импульс үшін k=1/2-ге тең:

6-сурет. Ұзақтығы екі есе кіші импульс АЖС тығыздығы

7-сурет. Ұзақтығы екі есе кіші импульс ФЖС тығыздығы

,

2.2.5 Сигналдың дискреттелуі

Дискреттелген сигнал санауларының толық саны:

Дискреттеу жиілігі:

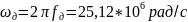
Сигналдың динамикалық жазылуын қарастырайық:

мұндағы, – Хэвисайд функциясын Дирак функциясымен алмастыру жасау үшін 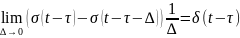теңдеуін қолдансақ болады.Сонда динамикалық теңдеу:

Сигналдың импульстік дискреттелуі тек қана нүктелерде ғана анықталған ( ). Сондықтан, интегралды k индексі бойынша қатарға түрлендіру қажет. Дифференциал ( 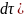дискреттеу қадамына (T) ауысады:

8-сурет. Дискреттелген сигнал

2.2.6 Дискреттелген сигналдың математикалық моделі

Жоғарыда келтірілген теңдеулерді ескеріп менің нұсқамда берілген сигнал үшін жалпы формуласы мына түрде болады:

Алынған теңдеуге мәндерді қойып

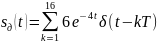
теңдеуін аламыз.

2.2.7 Дискреттелген сигналдың спектірлік тығыздығы

Айталық, s(t)= x(t)y(t) болсын. Ал олардың спектрлік тығыздығы:

,

болса, импульсті дискреттелген сигналдың спектрлік тығыздығы:

2.2.8 Дискреттелген сигналдың амплитудалық спектрі

9-сурет. Дискреттелген сигналдың амплитудалық спектрі

Қорытынды

Кейбір сигналдар цифрлық түрде беріледі, ал енді кейбіреуі аналогты түрде беріледі. Қазіргі таңда аналогты сигналдар нашар болғандықтан, оны цифрлық түрге түрлендіру қажет болады. Түрлендіру реті мынадай: дискреттеу, кванттау, цифрлық.

Берілген тапсырмада біз сынақ кітапшасының толық номерін ондық санақ жүйесінен екілік, сегіздік және он алтылық санақ жүйелеріне ауыстырдық. Сонымен қатар жоғарыда айтылған жүйелерден қайтадан ондық жүйесіне кері түрлендіру жасадық. Берілген жұмысты қортындылай келе біз келесідей шешімге келеміз: тура түрлендіру кезінде ең жеңіл түрлендіру түрі, ол – он алтылық санақ жүйесіне өту, ал кері түрлендіру кезінде, екілік санақ жүйесіне өту.

Екінші тапсырмада импульстің түріне сәйкес математикалық моделін, импульстың спектралды тығыздығын, АЖС және ФЖС сипаттамасын, ұзақтығы екі есе аз импульс үшін АЖС және ФЖС тәуелділігін, сигналды Т аралығымен дискреттеу, дискреттелген сигналдың математикалық моделін және спектралды тығыздығын, сондай-ақ дискреттелген сигналдың амплитудалық спектрын тұрғызып, зерттеулер жүргіздік. АЖС – бұл жұп функция, ФЖС – бұл тақ функция болып табылады.