Ячейка Содержимое

B8 = ((C9 + 2*C10)/8) –C8

B9 = ((10 – 5*C8 + 3*C10)/7)–C9B10 = ((2 + 2*C8 + C9)/2) –C10

Внесем в таблицу первое приближение для искомого решения. В ячейке С8 вве- дите значение 1 и скопируйте его в ячейки С9:С10. Далее следует сложить абсолютные значения уравнений в ячейках для построения оптимизируемой модулем поиска решения целевой функции. В ячейке, соответствующей це- левой функции, будет вычисляться сумма целого массива ячеек, поэтому она вводится с ^помощью клавишCtrl+Shift+Enter.

6. В ячейке С 12 введите следующуюформулу:

= СУММ(АВS(В8:В10)) и нажмите клавиши <Ctrl+Shift+Enter>.

6. Обведите ячейкиконтуром.

Приступим к решению системы с помощью модуля поиска решения.

6. Выберите команду Сервис >- Поискрешения.

7. ВполеУстановитьцелевуюячейкувведите$С$12,авполеИзменяяячейки—

- диапазон ячеек $С$8:$С$10. Включите переключатель Значению и введите в соответствующем текстовом поле значение 0. Щелкните на кнопке Вы- полнить для поиска решения.

Часть 2. Решение системы уравнений методами среды MathCad

Векторные и матричные операторы системы MathCad позволяют решать широкий круг за- дач линейной алгебры. Ниже приведен пример решения системы уравнений в матричной фор- ме.

Поскольку решение систем линейных уравнений довольно распространенная задача, то для этого в MathCad, начиная с шестой версии, введена встроенная функция

lsolve(A,B),

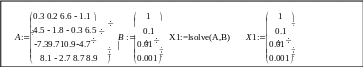которая возвращает вектор X для системы линейных уравнений A*X=B при заданной матрице коэффициентов А и векторе свободных членов В. Если урав- нений n , размер вектора В должен быть n, а матрицы A – n*n. Пример примене- ния этой функции также дан на рис.3.1.

Рис 3.1. Пример выполнения функции lsolve.

Порядок выполнения работы

1. В соответствия с номером варианта выбратьвходныеданные. Употреб- ляя два метода решенияуравнений

2. Выполнить расчеты . в средеMathCAD

3. Проанализировать полученные результаты и оформитьотчет.

4. Вариантызаданий

Задание. Решить систему уравнений с точностью до 0,0001.

№ 1.

3,21x ₁ - 4,25 х₂ +2,13х ₃= 5,06;

7,09х ₁+ 1,17х₂ - 2,23х ₃= 4,75;

0,43х₁ - 1,4х₂ - 0,62х ₃ = -1,05.

№ 3.

2,5х₁-3,12х₂ - 4,03х_з =-7,5;

0,б1х₁ + 0,71х₂ — 0,05х₃ = 0,44;

-1,03х₁—2,05х₂+0,877х_з = —1,16.

№ 5.

1,14х₁-2,15 х₂--5,11 х_з = —4,16;

-0,71х₁ +0,81 х₂-0,02 х_з = -0,17; 0,42х₁ - 1,1 З х₂ + 7,05 х_з == 6,15,

№ 7.

3,11 х₁ – 1,66х₂ - 0,60 х_з = —0,92;

-1,65х1 + 3,51 х₂ — 0,78 х_з = 2,57;

0,60 х₁ + 0,78 х₂ — 1,87хз == 1,65.

№ 9.

0,71 х₁ +0,10 х₂+0,12хз = 0,29;

0,10 х₁ +0,34 х₂—6,б4 х_з = 0,32;

0,12 х₁— 0,04 х₂ 0,1 х_з = -0,10.

№ 11.

0,12 х₁-0,43 х₂ +0,14хз= —0,17;

-0,07 х₁+0,34 х₂ +0,72хз= 0,б2; 1,18 х₁ - 0,08 х₂ - 0,25хз = 1,12.

№ 13.

0,66 х₁—1,44 х₂ —0,18 х_з =1,83;

0,48 х₁— 0,24 х₂ +0,37хз= — 0.84;

0,86 х₁+0,43 х₂ +0,64 х_з =0,64.

№ 15.

1,0 х₁+0,12 х₂+0,57 х_з =0,18;

0,38 х₁ + 0,2 х₂ — 54 х_з = 0,3;

0,28 х₁+0,46 х₂ —1,12 х_з =0,18.

№ 17.

0,10 х₁ — 0,04 х₂ — 0,13 х_з = —0,15;

-0,04 х₁ + 0,34 х₂ + 0,05 х_з = 0,31;

-0,13 х₁+0,05 х₂ +0,63 х_з =0,37.

№19.

1,20 х₁ — 0,20 х₂ + 0,30 х_з = — 0,60;

-0,2 х₁+1,6 х₂-0,1 х_з =0,30;

-0,30 х₁+0,10 х₂—1,5 х_з =0,40.

№ 21.

0,20 х₁ + 0,44 х₂ + 0,81 х_з = 0,74;

0,58 х₁ — 0,29 х₂ + 0,05 х_з = 0,02;

0,05 х₁ + 0,34 х₂ + 0,1 х_з = 0,32.

№ 2.

0,42х ₁1-1,13х ₂ + 7,05х_з = 6,15;

1,4х₁ -2,15х₂+5,11х_з = — 4,16;

-0,71х₁ +0,81х₂-0,02х_з = —0,17.

№ 4.

7,09х₁ +1,17х₂ — 2,23х_з = — 4,75;

0,43х₁ — 1,4х₂ — 0,62х₃= —1,05;

3,21 X_I — 4,25х₂ + 2,13х_з = 5,06,

№ 6.

0,61 х₁ + 0,71 х₂ - 0,05х_з = 0,44;

-1,03х₁-2,05 х₂+0,87х_з =—1,16; 2,5х₁ - 3,12х₂ - 5,03х_з = — 7,5.

№ 8.

0,10 х₁+12 х₂-0,13 х_з = 0,10;

0,12 х₁ + 0,71 х₂ + 0,15хз = 0,26;

-0,13 х₁+0,15 х₂+0,63хз=0,38.

№ 10.

0,34 х₁ - 0,04 х₂ + 0,1 х_з = 0,33;

-0,04 х₁ + 0,10 х₂ + 0,12 х_з = — 0,05;

0,10 х₁+0,12 х₂+0,71 х_з =0,28.

№ 12.

1,17 х₁+0,53 х₂—0,84хз=1,15;

0,64 х₁ - 0,72 х₂ - 0,43хз = 0,15;

0,32 х₁ + 0,43 х₂ - 0,93хз = — 0,48.

№ 14.

0,82 х₁ + 0,43х₂ - 0,57хз = 0,4 8;

-0,35 х₁+1,12 х₂-0,48хз=0,52;

0,48 х₁ + 0,23 х₂ + 0,37хз = 1,44.

№ 16.

1,16 х₁+1,3 х₂-1,14 х_з = 0,43;

0,83 х₁ -0,48 х₂—2,44 х_з = —0,15;

2 х₁-0,16 х₂+1,3 х_з =1,5.

№ 18.

0,63 х₁+0,05 х₂+0,15хз = 0,34;

0,05 х₁+0,34 х₂+0,10хз = 0,32;

0,15 х₁+0,10 х₂+0,71хз = 0,42.

№ 20.

0,30 х₁ + 1,20 х₂—0,20хз= —0,60;

-0,10 х₁—0,20 х₂+1,60хз = 0,30;

-1,50 х₁—0,30 х₂+0,10хз = 40.

№ 22.

6,36 х₁+11,75 х₂+10хз= —41,70;

7.42 х₁ + 19,03 х₂+11,75хз= —49,49;

5,77 х₁ + 7,42 х₂+6,36хз = —27,67.

№ 23.

0,40х₁+0,11х₂ +0,18хз =0,47;

0,28 х₁—0,59 х₂+0,03х_з =0,01;

0,02 х₁+0,24 х₂+0,10х_з =0,22.

№ 24.

0,18 х₁+0,25 х₂-0,44х_з =1,15;

0,42 х₁—0,35 х₂+1,12х_з =0,8б;

1,14 х₁+0,12 х₂-0,83 хз =0,68.

№ 25.

1,2 х₁+0,18 х₂ -0,42 х_з ==1,5;

0,44 х₁+0,36 х₂+0,12 х_з =1,16;

0,36 х₁-0,42 х₂-0,22 х_з = 0,15.

№ 26.

0,64 х₁—0,43 х₂+0,57 х_з =0,43;

0,56 х₁ + 0,12 х₂ — 0,27 х_з = 0,88;

0,63 х₁ - 0,83 х₂ + 0,43 х_з = — 0,12.

№ 27.

1,60 х₁+2,18 х₂—0,72 х_з =1,15;

0,43 х₁ — 0,16 х₂ + 0,53 х_з = 0,53;

0,34 х₁ + 0,57 х₂ — 0,83 х_з = — 0,42.

№ 28.

0,8 х₁ — 0,13 х₂ + 0,63 х_з =1,15;

0,42 х₁ + 0,57 х₂ + 0,32 х_з == 0,84;

0,54 х₁ + 0,62 х₂ - 0,32 х_з == 0,25.

№ 29.

1,06 х₁-0,28 х₂ +0,84 х_з =0,57;

0,43 х₁ + 0,62 х₂ — 0,35 х_з = 0,66 ;

0,37 х₁— 0,75 х₂ — 0,64 х_з =— 0,38.

№ 30.

0,75 х₁ - 0,84 х₂ +1,11 х_з == 0,66;

1,12 х₁ -0,14 х₂ +0,45 х_з =0,83;

0,32 х₁ +0,23 х₂ -0,48х_з=0,14.

4. Содержаниеотчета

1. Формулировказадания.

2. Краткие теоретические сведения о примененномметоде.

3. Описание процесса выполнения работы и результатырасчетов.

4. Выводы.