2. Интерполирование для случая равноотстоящих узлов. Первая ивто- рая интерполяционные формулыНьютона

Узлы интерполяции называются равноотстоящими, если

X_i+1 – x_i= x_i= h=const ( i= 0,1, .,п—1).

Конечными разностями функции y = f(x) называются разности вида

 y_i = y_i+1 + y_i - конечные разности первого порядка,

² y_i = y_i+1 + y_i - конечные разности второго порядка,

^k y_i = ^k-1 y_i+1 + ^k-1 y_i —конечные разности k-го порядка.

Первая интерполяционная формула Ньютона имеет вид

Ух Р_n

х) y₀

• gy₀

_g( g  1) _{2 y}

2! ⁰

_....g( g  1)....(g n  1) _,

n!

где

_{g }x x_{0 .}

h

Вторая интерполяционная формула Ньютона имеет вид

Yx P

10. y g y

g(g1) _2y

....

g(g1)....(gn1) _{n ,}

 _n 

 _n 

^n 1 ^

 _{n 2} 

2!

y ₀

n!

где

_{g }x x_{n .}

h

Интерполяционная формула Лагранжа

Приведенные выше формулы пригодны лишь в случае равноотстоящихузлов интерполирования. Дляпроизвольнозаданных узлов интерполирования пользуются более общей формулой, так называемой интерполяционной форму- лойЛагранжа.

Пусть на отрезке [а, b] даны n + 1 различных значений аргумента: х₀, x₁ х₂ , ...,

х_п и известны для функции y = f(x) соответствующие значения: y₀ , y₁ , y₂ … y_n .

Требуется построить полином L_n (x) степени не выше п, имеющий в заданных узлах х₀, x₁ х₂ , ..., х_п те же значения, что и функция f(x), т. е. такой, что

L_n (x_i )=y_i ( i = 0, 1, 2, …. n).

ⁿ (x x

)(xx)...(xx

)(xx

)...(x x )

L_n(x)_y_i

0 1 i1 i1 n

i  0

(x_i x₀ )(x_i x₁)...(x_i x_{i 1}) (x_i x_{i 1})...(x_i x_n )

Следует отметить, что формула Лагранжа в отличие от предыдущих интерпо- ляционных формул содержит явно y_t, что, бывает иногда важно.

Рассмотрим два частных случая интерполяционного полинома Лагранжа.

При n = 1мы имеем две точки, и формула Лагранжа представляет в этом слу- чае уравнение прямой у = L₁(х), проходящей через две заданные точки:

где а, b —абсциссы этих точек.

При п = 2 получим уравнение параболы y = L₂(x), проходящей через три точ- ки:

где а, b, с — абсциссы данных точек.

Пример 1, Для функции у = sin х построить интерполяционный полином Лагранжа, выбрав узлы

Решение. Вычисляем соответствующие значения функции:

Применяя формулу (5), получим:

или

2.Порядок выполнения работы

1. Составить таблицу в “Excel” для вычисления конечных разностей согласно табл.2.1.

2. Используя первую или вторую интерполяционную формулу Ньютона, вы- числить значения функции при данных значенияхаргумента в табл.2.2.

3. Построить диаграммуфункции.

4. Используя команды меню “Excel” Диаграмма  Добавить линиютренда построить точечную диаграмму с приведением значений аппроксимирую- щегополинома.

3. Примервыполнения

X	Y	Yi	Yi_2	Yi_3
0,45	4,4817	0,4713	0,0496	0,0052
0,46	4,953	0,5209	0,0548	0,0058
0,47	5,4739	0,5757	0,0606	0,0063
0,48	6,0496	0,6363	0,0669	0,007
0,49	6,6859	0,7032	0,0739	0,0078
0,5	7,3891	0,7771	0,0817	0,0087
0,51	8,1662	0,8588	0,0904	0,0094
0,52	9,025	0,9492	0,0998	0,0105
0,53	9,9742	1,049	0,1103	0,0116
0,54	11,0232	1,1593	0,1219
0,55	12,1825	1,2812
0,56	13,4637

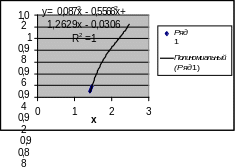
Рис.2.2 Таблица с конечными разностями.

Рис.2.3. Диаграмма функции с вычисленными значениями коэффициентов аппроксимирующего полинома.

3. Вариантызаданий

Таблица № 1с данными для интерполирования

Вариант № 1		Вариант № 2		Вариант № 3		Вариант № 4		Вариант № 5
x	y	x	y	x	y	x	y	x	y
1,415	0,888551	0,101	1.26183	0,15	0,860708	0,180	5,61543	3,50	33,1154
1,42	0,889599	0,106	1,27644	0,20	0,818731	0,185	5,46693	3,55	34,8133
1,425	0,890637	0,111	1,29122	0,25	0,778801	0,190	5,32634	3,60	36,5982
1,43	0,891667	0,116	1,30617	0,30	0,740818	0,195	5,19304	3,65	38,4747
1,435	0,892687	0,121	1,32130	0,35	0,704688	0,200	5,06649	3,70	40,4473
1,44	0,893698	0,126	1,33660	0,40	0,670320	0,205	4,94619	3,75	42,5211
1,445	0,894700	0,131	1,35207	0,45	0,637628	0,210	4,83170	3,80	44,7012
1,45	0,895693	0,136	1,36773	0,50	0,606531	0,215	4,72261	3,85	46,9931
1,455	0,896677	0,141	1,38357	0,55	0,576950	0,220	4,61855	3,90	49,4024
1,46	0,897653	0,146	1,39959	0,60	0,548812	0,225	4,51919	3,95	51,9354
1,465	0,898619	0,151	1,41579	0,65	0,522046	0,230	4,42422	4,00	54,5982
				0,70	0,496585	0,235	4,33337	4,05	57,3975
				0,75	0,472367			4,10	60,3403
								4,15	63,4340
								4,20	66,6863
Вариант № 6		Вариант № 7		Вариант № 8		Вариант № 9		Вариант № 10
x	y	x	y	x	y	x	y	x	y
0,115	8,65729	1,340	4,25562	0,01	0,991824	0,15	4,4817	0,45	20,1946
0,12	8,29329	1,345	4,35325	0,06	0,951935	0,16	4,9530	0,46	19,6133
0,125	7,95829	1,350	4,45522	0,11	0,913650	0,17	5,4739	0,47	18,9425
0,13	7,64893	1,355	4,56184	0,16	0,876905	0,18	6,0496	0,48	18,1746
0,135	7,36235	1,360	4,67344	0,21	0,841638	0,19	6,6859	0,49	17,3010
0,14	7,09613	1,365	4,79038	0,26	0,807789	0,20	7,3891	0,50	16,3123
0,145	6,84815	1,370	4,91306	0,31	0,775301	0,21	8,1662	0,51	15,1984
0,15	6,61659	1,375	5,04192	0,36	0,744120	0,22	9,0250	0,52	13,9484
0,155	6,39986	1,380	5,17744	0,41	0,714193	0,23	9,9742	0,53	12,5508
0,16	6,19658	1,385	5,32016	0,46	0,685470	0,24	11,0232	0,54	10,9937
0,165	6,00551	1,390	5,47069	0,51	0,657902	0,25	12,1825	0,55	9,2647
0,17	5,82558	1,395	5,62968	0.56	0,631442	0,26	13,4637	0,56	7,3510
0,175	5,65583
0,18	5,49543

Таблица № 2 Данные аргумента,при которых следует определить значение функции

№ вари- анта	Значение аргумента
	X1	X2	Х3	X4
1.	1,4161	1,4625	1,4135	1,470
2.	0,1026	0,1440	0,099	0,161
3.	0,1511	0,7250	0,1430	0,80
4.	0,1817	0/2275	0,175	0,2375
5.	3,522	4,176	3,475	4,25
6.	0,1217	0,1736	0,1141	0,185
7.	1,3617	1,3921	1,3359	1,400
8.	0,027	0,525	0,008	0,61
9.	0,1539	0,2569	0,14	0,2665
10.	0,455	0,5575	0,44	0,5674
11.	1,4179	1,4633	1,4124	1,4655
12.	0,1035	0,1492	0,096	0,153
13.	0,1535	0,7333	0,100	0,7540

3. Содержаниеотчета

1. Формулировказадания

2. Описание процесса выполнения работы и результатырасчетов.

3. Диаграмма функции с вычисленными значениями коэффициентов аппрок- симирующегополинома.

4. Выводы.