Лабораторная работа № 12

Тема: Моделирование сигналов произвольнойформы

Цель работы: научиться моделировать сигналы по рядам Фурье ме- тодами среды MathCAD

1. Вводные замечания.

В механике, термодинамике, электротехнике и радиотехнике встречаются временные зависимости с самой различной формой. Именно поэтому одно из фундаментальных положений математики, ранее казавшимся абстрактным а за- тем нашедшим широчайшее практическое применение, является возможность описания любой периодической функции, имеющей конечное число разрывов и непрерывность производных между ними, с помощью тригонометрического ря- да Фурье [7,8 ]

N

Y(t) _a_k sin2f1tb_k cos(2f1t)

k 1

где k — порядковый номер гармоники, f1 — частота колебания Этот ряд со держит бесконечное число косинусных и синусных составляющих — гармоник, причем амплитуды этих составляющих а_k и b_k являются коэффициентами Фурье, определяемыми приводимыми несколько позднее интегральными выражениями .

Приведенный ряд содержит бесконечное число членов и при таком представ- лении оказывается бесполезным, поскольку время вычисления в этом случае так- же равно бесконечности. К счастью, амплитуды гармоник для реальных зависи- мостей y (t) довольно быстро уменьшаются по мере роста номера гармоники k.

Поэтому на практике обычно приходится иметь дело с ограниченными по числу гармоник рядами Фурье.

Помимо упомянутой формы ряд Фурье можно представить в виде:

N

Y(t) _M_k cos(2f1t _k )

k 1

где амплитуда гармоник М_k и их фаза _k определяются выражениями:

M_k и _k = -arctan(b_k/a_k).

Преимущество ряда в этой форме в том, что для вычисления каждого члена ряда нужно лишь один раз обращаться к довольно медленному вычислению тригонометрической функции. В дальнейшем будут приведены формулы, по- зволяющие вычислять коэффициенты Фурье (либо амплитуды и фазы гармоник) для любой функции y (t). Это является задачей спектрального анализа. Здесь же мы рассмотрим обратную задачу — синтеза зависимости y (t) путем вычисления ряда Фурье с ограниченным числом членов.

Теория спектрального анализа и синтеза хорошо развита, и для многих зави- симостей y (t) заведомо известны значения коэффициентов Фурье или законы изменения (с частотой или номером гармоники) амплитуд и фаз гармоник. Это позволяет синтезировать наиболее распространенные зависимости y (t).

Встроенные в систему MathCAD средства быстрого преобразования Фурье (БПФ) существенно упрощают процедуру приближенного спектрального анали- за. БПФ — быстрый алгоритм переноса сведений о функции, заданной 2ⁿ отсче- тами во временной области, в частотную область. Если речь идет о спектраль- ном анализе функции y (t), ее нужно задавать действительными отсчетами и ис- пользовать функцию fft (V), где V — вектор, элементы которого хранят отсчеты функции y (t). Результатом будет также вектор А с комплексными элементами

• отсчетами в частотной области (их вдвое меньше, чем отсчетов во временной области). Фактически действительная и мнимая части этого вектора есть коэф- фициенты Фурье b_k и a_k что существенно упрощает ихполучение.

Казалось бы, наличие встроенных средств широко рекламируемого БПФ должно означать ориентацию спектрального анализа на их применение. Но это не так. БПФ имеет ряд серьезных недостатков: неясный для пользователя алго- ритм, отсутствие средств подавления эффекта Гиббса и строгая привязка числа отсчетов y (t) к величине 2n (т. е. 2, 4, 8, 16, 32 и т. д.). БПФ дает хорошие ре- зультаты, когда взаимное преобразование (прямое и обратное) происходит без ограничения употребляемого при нем количества гармоник. Эти недостатки мо- гут оказаться весьма существенными при проведении спектрального анализа и синтеза, когда наглядность их реализации принципиально важна.

В основе так называемого стандартного спектрального анализа лежит вычис- ление интегралов, определяющих коэффициенты Фурье, простейшим числен- ным методом прямоугольников Может показаться, что это большой шаг назад в сравнении с классическим методом. И уж тем более трудно поверить, что такой метод является единственным научно обоснованным методом вычисления этих коэффициентов [7, 8] Тем не менее это так. И понятно, почему. Если функция y

(t) задана рядом дискретных отсчетов (вектор Yi), мы не имеем права предпола- гать, что какая-либо интерполяция значений y (t) между узлами имеет преиму- щество перед постоянством y (t). Строгий теоретический анализ показывает, что синтез у(t) по максимальному для данного числа отсчетов количеству гармоник при интегрировании методом прямоугольников дает наименьшую среднеквад- ратичную погрешность.

Для реализации этого метода сначала зададим вектор-строку исходных отсче- тов y(t):

Yi  ( 0 0 0.5 0.5 1 1 1 1 1 0 0 0 0 0 0 0 0 0 00 )

и исходные данные:

f1  250000

частота ^{M 23}

число гармоник.

Далее осуществим линейную интерполяцию

1

Yi

Y ^T

Ni

length(Y)

dt 

f1Ni

i

0  Ni  1

ti_iidt

y(t)  linterp(ti Y t)

Тогда численный спектральный анализ осуществляется следующим образом:

N2M

dt 

1

f1N

i

0  N  1

Y_i

y(idt)

p2f1dt

k  0  M

j 

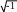При вычислении коэффициентов A_k и B_k для максимального ускорения про- цесса вычисления нужно исключить бесполезные умножения на нулевые отсчеты функции – их результат тождественен 0 :

^A_k^_^if^Y_i ^00Y_i^{cos(pki)}

i

^B_k^_^if^Y_i ^00Y_i^{sin(pki)}

i

Амплитуду M_k k-ой гармоники и фазу _k вычисляем по формулам

² 

M_k 

A_kjB_k



^N

^_k^arg^A_k^jB_k

Спектральный синтез осуществляется по формуле

A₀

^{F(t)  if}^M_k ^00M_k^cos^{p1kt}_k

_N 

k

Графики полученных зависимостей представлены на рис

0.6

M_k

0.6

0.4

0.2

₄ 4

		i

2

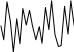
_k 0

2

0 ₀

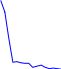
0 4 8 12 16 20

 4 ₄

0 5 10 15 20 25

0 k 20 0 k 25

Рис 12.1. Зависимости амплитуд и фаз гармоник от ихномера.

1.1

0.8

Y_i

0.5

F(idt)

0.2

 0.1 _0.1

0 10 20 30 40

0 i 40

Рис 12.2. Форма исходного и синтезированного сигналов.

2.Порядок выполнения работы

1. В соответствия с номером варианта выбрать входные данные. Упот- ребляя изложенные выше методы решения вычислить ФЧХ, АЧХ и переходную характеристики системы методами среды MathCAD.

2. Выполнитьрасчеты в средеMathCAD

3. Вывести награфики.

4. Проанализировать полученные результаты и оформитьотчет.

3.Bapиaнты заданий

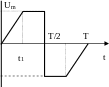
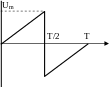
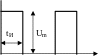
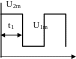
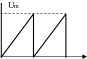Рис.12.3 Рис.12.4 Рис.12.5

T/2 T

T T

Рис.12.6 Рис. 12.7 Рис.12.8

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Рис	3	4	5	6	7	8	3	4	5	6	7	8	3	4	5	6	7	8	3	4
Т(мсек)	10	20	30	40	50	10	20	30	40	50	10	20	30	40	50	10	20	30	40	50
tи (t1 )	2			10	25		5			10	4		6			2	8		10
Um (U2m )	4	6	8	10	12	14	16	18	20	4	6	8	10	12	14	16	18	20	4	6
U1m	-	-	-	-	6	-	-	-	-	-	2	-	-	-	-	-	10	-	-