4. Содержание отчета

1. Формулировказадания

2. Описание процесса выполнения работы и результатырасчетов.

3. Выводы.

Лабораторная работа № 10

Тема: Моделирование АЧХ и ФЧХ по операторной функции линейной сис- темы

Цель работы: научиться вычислять АЧХ и ФЧХ по операторной функции линейной системы методами среды MathCAD

1. Вводныезамечания.

Многие физические объекты или системы (механические, электрические, акустические и другие) находятся под воздействием гармонических возмущений. Если такие системы линейны, то их поведение от частоты возмущения описыва- ется амплитудно-частотными характеристиками (АЧХ) и фазочастотными харак- теристиками (ФЧХ) . Они вычисляются с применением операторного метода.

Для вычисления АЧХ и ФЧХ достаточно заменить оператор p на величину j, тогда модуль полученного выражения будет описывать АЧХ, а аргумент – ФЧХ.

Рассмотрим построение АЧХ и ФЧХ для системы второго порядка, описан- ной следующей передаточной функцией:

K ( p) :

K _.

T ² p ²  2Tp  1

Задав мнимуюединицу

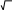j 1

и введем следующие соотношения:

i 0  20

w_i 

314. i

p_i 

w_i j

Тогда АЧХ системы будет описываться выражением |K(p)|.

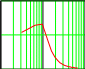
График Ачх представлен на рис.10.1.

2

1.312

^K^p_i ¹

0.026 ₀

0.1 1 10

0.314 _wi

6.28

Рис.10.1.Логарифмическая АЧХ системы.

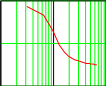
ФЧХ системы задается выражением arg(K(p)) а график представлен на рис.10.2.

0.272 ⁰

^arg^K^p_i ²

3.012

4

0.1 1 10

0.314 _wi

Рис.10.2 График ФЧХ системы

6.28

Переходная характеристика системы вычисляется из следующего интеграль- ного выражения (в нем бесконечный верхний предел заменен конечным, с рос- том которого h(t) практически перестает меняться):

6



h(t)  0.637 ^



₀

Re(K(w j)) 

sin(w t)

dw

w

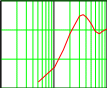
Задав i=0.. 10 и t_i = 0.5*i находим h_i :=h(t_i ). Переходная характеристика сис- темы показана на рис.10.3.

1.254

h_i 0.105

1.5

1

0.5

0

0.1 1 10

0.5 t_i 10

Рис. 10.3. График переходной характеристики системы.

2.Порядок выполнения работы

1. В соответствия с номером варианта выбрать входные данные. Упот- ребляя изложенные выше методы решения вычислить ФЧХ, АЧХ и переходную характеристики системы методами среды MathCAD.

2. Выполнитьрасчеты в средеMathCAD

3. Вывести награфики.

4. Проанализировать полученные результаты и оформитьотчет.

3.Варианты заданий

№ варианта	K(p)
	Т		К
1.	0.6	0.1	2
2.	0.6	0.2	2
3.	0.6	0.3	2
4.	0.6	0.4	2
5.	0.6	0.5	2
6.	0.6	0.6	2
7.	0.8	0.1	3
8.	0.8	0.2	3
9.	0.8	0.3	3
10.	0.8	0.4	3
11.	0.8	0.5	3
12.	0.8	0.6	3
13.	0.4	0.1	2
14.	0.4	0.2	2
15.	0.4	0.3	2
16.	0.4	0.4	2
17.	0.4	0.5	2
18.	0.4	0.6	2