Поиск точки минимума



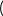
₂ 2

z 1 y(x) 50 x z z

x_опт мин_З_С( y 10 10) x_опт1

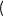
yx_опт 1

3. Поиск минимума функции с помощью оператораGiven

x 1

y 6

3

f(xy)50(xy)²50y

Здание функции

_Given Начло вычисленияминимума

^d f(xy) 0 dx

^d f(x y) dy

₀ Условияминимума

x

MinErr(xy) ^{Поиск минимума с помощьюфункции}minerr

y

x 2.035 10 ¹⁰

f(x y) 0

y 2.035 10 ¹⁰

Проверка решения

3. Поиск минимума функции с помощью оператораFind

x 1

y 6

3

F(x y) 50(x y)²50yGiven

Здание функции

^d F(xy) 0 dx

^d F(xy) 0 dy

_x1

^y1



Find(xy)



Поиск минимума с помощью функции Fin

x1 y1

Варианты заданий

12.4.Bapиaнты задач

№	Экс- тремум	Функция F (X , Y )
1	Min	50(X -Y2 )2 - Y
2	Min	100 (Y -X2 )2 + (1 - X )2
3	Min	(X3 - XY + Y2 ) / e -X
4	Min	3X2 + 4XY + 5Y2
5	Min	40 (X -Y2 )2 + ( 1 - X )2
6	Min	50 (X2 -Y )2 + ( 1 - Y )2
7	Min	(X2 -Y )2 + 50( 1 - Y )2
8	Min	e -X – e -2X + e -10Y
9	Min	X Y2 / e (X - Y)
10	Min	(10X3 - XY + 8Y2 ) / e -X
11	Min	(e -0. 1X - e -2X + e -10Y ) 2
12	Min	e ( X – Y) / (2 + XY)
13	Min	X4 – 4X2Y + X2 + 4Y2 - 6X +2
14	Min	(x3 – xy + y2 )e -1/x
15	Min	(25X3 - XY + 10Y2 ) / e -X
16	Min	0,1 X3 - 2X2 + 10Y2
17	Min	e -0. 1X - e -2X + e -10Y
18	Min	(10X3 - XY + 8Y2 ) / e -X
19	Min	(30X2 - XY + Y3 ) e Y
20	Min	(X – 5 ) e Y
21	Min	e ( X – Y) / (Y - X2 )
22	Min	100e ( X - Y) / (20 + YX2 )
23	Min	2X2 + XY + Y2 + 2X + Y + 1
24	Min	e ( X – Y) / (3 + YX2 )
25	Min	100e ( X - Y) / ( 10 + YX2 )

8.4. Содержание отчета 1.Тема и цель работы

2.Краткие теоретические сведения о примененном методе 3.Описание процесса выполнения работы и результаты расчетов. 4.Выводы.

Лабораторная работа № 9 Тема: Решение дифференциального уравнения первого порядка ме- тодом Рунге — Кутта

1. Вводныезамечания.

Решение дифференциальных уравнений широко применяется в практике на- учно-технических расчетов Это связано с тем, что дифференциальные уравнения (и системы из них) часто являются наиболее простым аппаратом для построения моделей динамических процессов, т.е. описывают поведение различных объек- тов в динамике, например переходные процессы в электронных схемах или рабо- ту часового маятника. Линейные дифференциальные уравнения имеют решения в виде специальных функций (скажем, функций Бесселя). Однако многие физи- ческие системы нелинейные и описываются нелинейными дифференциальными уравнениями, не имеющими аналитического решения. В этом случае приходится использовать численные методы решения дифференциальныхуравнений.

Версия MathCAD 8 PRO содержит мощные средства для реализации числен- ных методов решения дифференциальных уравнений. Поэтому может возник- нуть вопрос: а нужно ли создавать свои документы для реализации таких мето- дов? Ответ на него не однозначен. Если ваша цель — решение конкретной зада- чи, то проще воспользоваться готовыми функциями MathCAD. Они описаны в литературе. Однако нередко педагоги и специалисты без должных оснований го- ворят о трудности реализации в системе MathCAD обычных численных методов. Это неверно! Реализация таких методов в системе MathCAD легка и наглядна.

Более того, она позволяет вмешиваться в алгоритмическую реализацию методов решения, что способствует созданию новых или улучшенных методов решения дифференциальных уравнений, ориентированных на решение интересующих пользователя задач.

Здесь мы остановимся на реализации решения дифференциальногоуравнения i/=f (x, y) хорошо известным методом Рунге — Кутта. Пусть h — шаг прираще- ния переменной х, i — индекс, имеющий значения от 1 до N (N — число интерва- лов решения с шагом h). Метод Рунге — Кутта четвертого порядка дает погреш- ность решения порядка h (4, что удовлетворяет самым придирчивым требовани- ям к точности численных методов. Он неоднократно подробно описывался в [6, 8, 14]. Его реализация показана на рис.9.1.

Рассматривая рис 9.1, нетрудно сделать вывод о наглядности реализации ме- тода Рунге — Кутта. По существу приведенные уравнения повторяют известные формулы этого метода часто встречающиеся в учебной литературе по численным методам решения дифференциальных уравнений.

РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГОУРАВНЕНИЯ y'=f(x,y) МЕТОДОМ РУНГЕ-КУТТА

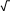
f(x y) 

y _y

2

Основное уравнение - выражение для производной

x 1

startx 0

endx 15

n 200

inity 0.5

Исходные данные

Реализация метода Рунге-Кутта:

k1(xy h) f(x y)

k2(xyhhd) f(xhdyhdk1(xyh))

k3(xyhhd) f(xhdyhdk2(xyhhd))

k4(xyhhd) f(xhyhk3(xyhhd))

rk(xyhhd)_k1(xyh)2k2(xyhhd)  _

x₀ startx

^{2k3(xyhhd)k4(xyhhd)} 

_hendxstartx _hd0.5h n

j 1 n

x_jstartxjh

y₀ inity

^y_j^y_j1^rk^x_j1^y_j1^hhd^h

⁶ 

L floor(min(y) .5) k 0 n

U

y_k

U ceil(max(y) .5)

U 

График решения

L

startx x_k

L 

endx

Рис. 9.1. Реализация метода Рунге-Кутта:

Решение дифференциального уравнения с использованием функции Rkadapt.

y 0

y'2ysin(x) 0 y₀ 2

D(xy)2ysin(x)

начальное приближение

первая производная

n 200

x1 0

x2 10

ZRkadapt(yx1x2nD)

решение с переменным шагом

x Z

₀

y Z

₁

i 0 n 1

y_i

x_i

2.Порядок выполнения работы

1. В соответствии с номером варианта выбрать входныеданные.

2. Выполнить расчеты . в средеMathCAD

3. Проанализировать полученные результаты и оформитьотчет.

3.Варианты заданий

№ п/п	Диф. Уравнение	Начальные условия
1	Y’ – 0,8∙X2 - Y = 0	0,5
2	(Y- Y2)Y’ = 1 – X	0,3
3	Y’/tg(2X) = 2	0,1
4	Y*Y’ = (1 – 2X)/Y	0,7
5	X*Y’ + Y = Y2	0,5
6	Y= Sin(Y) +Cos(X)	0,8
7	Y’ = 2YSin(X2)	0,6
8	2YY’ = Sin(X2)	0,2
9	Y’ =e(Sin(X))	0,5
10	Y’ + sin((X+Y)/2) = 0	0,3
11	Y’sin(X) = Yln(Y)	0,1
12	Y’ = (1 - Y)/ (1 + X2 )	0,7
13	Y’ = cos(Y)- sin(X)	0,5
14	Y – X Y’ = 2.4 (1 + X2 Y’)	0,8
15	Y’ = cos(X – Y)	0,6
16	Y’ = 3X – 2Y +5	0,2
17	Y ' 1X Y X Y 1	0,5
18	Y’= 0,2YeSin(6X)	0,3
19	Y’= 5Ytg(5X)	0,1
20	Y’ = X / (Y – X2)	0,7
21	Y’= 2Y tg(2X)	0,5
22	Y’ = X/Y + Y/X	0,8
23	Y’ = eY/X +Y/X	0,6
24	(Y - X2 )Y’ = X	0,2
25	(X2 + 1) Y’ = Y lg(Y)	0,5
26	Y’ = Y / X	0,8
27	3Y2 + 3XY + X2 = Y’ (X2 + XY)	0,6
28	Y’ – arctg(Y/X) = X	0,2