Лабораторная работа № 7

Тема: Обработка данных. Аппроксимация

Цель работы: научиться обрабатывать табличные - заданные функции методами среды MathCad

1. Вводныезамечания.

Наиболее распространенным и практически важным случаем, когда вид свя- зи между параметрами х и у неизвестный, есть задача этой связи в виде некото- рой таблицы (х,у), это означает, что дискретному множеству значений аргумента

{х} соответствует множество значений функции {y}( i = 0,l,... ,n). Эти значения - или результаты расчета, или экспериментальные данные . На практике нам мо- гут понадобиться значение величины у и в иных точках , отличных от узлов . Но получить эти значения можно лишь путем очень трудных расчетов или проведе- нием дорого эксперимента.

Таким образом, с точки зрения экономии времени и способов мы приходим к необходимости использования табличных данных которые имеем, для при- ближенного расчета искомого значения функции при любом значении ( с неко- торой области ) параметра х , поскольку точная связь y=f(x) неизвестна. В среде MathCAD есть для этой цели инструментарий :

• способы линейной аппроксимации (функцияlinterp);

• аппроксимация сплайном (interp), линейная (Ispline), параболическая (pspline). кубическая (cspline)).

2.Пример аппроксимации таблично заданной функции способами MathCad.

Представим исходную табличную функцию в виде

_1.9 _

^1.5 ^

 

 ⁴ 

 ₁ 

 

_1.9 4 _

^1.5 1 ^

 

³ 

_17 _

_3 17 _

x y data

^4 ^

^ 9 ^

^4 9 ^

^5.5 ^

 

_6.2 _

₂₃ 

 

_35.5 _

^5.5



_6.2

23 ^



35.5 _

datacsort(data0)

X data

^0^

Y data

^1^

х - значения аргумента; у - значения функции.

Исходные данные перед дальнейшей обработкой необходимо отсортировать по возрастанию аргумента - значений х . Воспользуйтесь функцию сортирования CSORT, которая сортирует матрицу по указанном столбцу . Для этого оба век- торы х и у объединим в матрицу data с двумя столбцами .

1. Линейнаяаппроксимация

fit(x) linterp(X Yx)

fit(2) 5.182

^{fit(7.71)62.464} i 0 length(X) 1

При оформлении графика необходимо выставить следующие параметры

График линейной интерполяции таблично заданной функцииизображенныйна рис. 1.1

40

35.5

30

20

Y_i ^fit^X_i

10

1 ₀

1 2 3 4 5 6 7

1.5 _Xi

Рис. 1.1. Линейная аппроксимация

6.2

2. Аппроксимациясплайном

Параболическим:

pvs = pspline (VX,VY) Ky6ическим:

cvc=cspline(VX,VY) Kub(x ) = interp (cvc , VX, VY, x)

data  csort(data 0)

Вычисление

VX  data

⁰

VY  data

¹

коэффициентовсплайна: Интерполирующая

S  cspline(VX VY)

_{функция:} Kub(x)  interp(S VX VYx)

Примеры интерполированных

Kub(2)

5.33

значений:

Kub(7.71)

42.029

i 

0  length(VX) 1

scale

100

j 0  scale

x_j  min(VX)  j 

max(VX) min(VX) scale

Результаты аппроксимации кубическим сплайном в сравнении с линейною

интерполяциею представлены на рис 1.2

40

35.5

30

20

VY_i ^Kub^x_j

10

1 ₀

1.5 2 2.5 3 3.5 4 4.5 5 5.5 6 6.5

1.5

X-Y

interpolir

VX_i x_j

6.2

Рис. 1.2. Результаты аппроксимации кубическим сплайном

ПОЛИНОМИАЛЬНАЯ АППРОКСИМАЦИЯ

1.9	4		1.9	4
1.5	1		1.5	1
3 17 3 Y data				17
4	9	4		9
5.5	23	5.5		23
6.2	35.5	6.2		35.5

Ввод данных для интерполяции

X

n rows( data) n 6

^{Степеньполинома} k 3

z regress( XYk)

		(coef	fs T )		59
i	0 n	1	j		0	50	txj	min(X)

fun(x) interp( zXYx) coeffs submatrix( z3length(z) 100)

.109 61.621 17.237 1.578

_jmax(X) min(X)

50

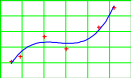40

30

Y

i ²⁰

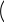
fun tx

_j 10

0

10

1 2 3 4 5 6 7

Xtx

i j