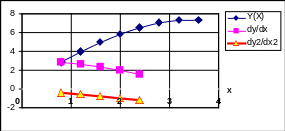
3. Пример выполнения задания представленниже.

Ниже приведен пример вычисления первой и второй производной и построения соот- ветствующих графиков.

X	Y(X)	 yi	 yi	 yi	dy/dx	dy2/dx2
0,8	2,857	1,089	-0,097	-0,032	2,81711	-0,40625
1,2	3,946	0,992	-0,129	-0,032	2,61461	-0,60625
1,6	4,938	0,863	-0,161	-0,034	2,330445	-0,79375
2	5,801	0,702	-0,195	-0,034	1,970445	-1,00625
2,4	6,503	0,507	-0,229	-0,036	1,52378	-1,20625
2,8	7,01	0,278	-0,265
3,2	7,288	0,013
3,6	7,301

3. Содержаниеотчета

1. Формулировказадания

2. Описание процесса выполнения работы и результатырасчетов.

3. Диаграмма.

Лабораторная работа № 6

Тема: численное интегрирование функций

1. Вводныезамечания.

Наиболее часто при численном интегрировании используются правило пря- моугольников, правило трапеций, правило Симпсона и квадратура Гаусса. Каж- дый из этих методов является более точным, чем предыдущий, поскольку произ- водит аппроксимацию данных более сложной кривой.

Правило прямоугольников

Согласно правилу прямоугольников, область между точками заполняется прямоугольником, высота которого соответствует координате у одной из точек, а ширина равна расстоянию между точками. Значение интеграла определяется по следующей формуле:

n 1

I _y_i (x_i1 x_i )

i1

Такое приближение может показаться очень грубым, например, для случая, указанного на рисунке, однако при малой ширине интервала и гладкой функции результаты получаются достаточно точными. Кроме того, такой метод очень просто реализовать, поскольку достаточно просто перемножить данные в каж- дой точке на ширину интервала и сложить результат.

Правило трапеций

Согласно этому правилу, каждая пара соседних точек соединяется прямой линией, образуя последовательность трапеций.

n1

I _

i 1

^yi ^yi1 _{( x}

2

i1

• x_i)

Площадь трапеции равняется полусумме оснований, умноженной на высоту

• расстояние между точками в данном случае. Общий интеграл равняется сумме площадей всехтрапеций.

Основу машинных алгоритмов интегрирования составляет геометриче-

b

ский смысл определенияинтеграла

y _f (x)dx

a

- площади, ограниченной

подынтегральной кривой f(x), осью абсцисс и ординатами f(a) и f(b).

Вычисление по формуле Симпсона осуществляется по следующему

многочлену :

I = h/3{ y₀ + y₁ + 4(y₁ + y₃ + y₅ + y₇) +2(y₂ + y₄ + y₆)},

Где y_i = y(x_i) ; x_i = a + ih (i = 0,1,….); h = (b – a )/ n. Для расчетов принимаем n = 8.

2. Пример использования методовинтегрирования

Использование методов интегрирования достаточно просто. В каждой ячейке происходит вычисление значения интеграла между двумя точками. В последней ячейке все эти значения суммируются.

В следующем примере, вычислите гамма- функцию с помощью численного интегрирования. Используйте все методы, описанные ранее, и сравните резуль- таты.

Гамма -функция

Гамма-функция принадлежит к так называемым специальным функциям науки и техники. Она возникает в физических задачах, например, при вычисле- нии вероятностей в статистической механике или при нормировке волновых функций в кулоновском поле. При целых значениях аргумента гамма-функция становится обычным факториалом.

Г(n+1) = n!

Гамма-функция определяется следующим интегралом

Г(x) 



20. 

    _t x1_dt

0

не имеющим аналитического выражения. Значения гамма- функции обычно задаются таблично.

В следующем примере, вычислите гамма- функцию с помощью численного интегрирования. Используйте все методы, описанные ранее, и сравните резуль-

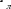таты. Значение гамма- функции в точке х =1,5равно .

2

Используйте именно такое значение х, чтобы сравнить результаты ин- тегрирования с правильной величиной.

1. Создайте новый рабочий лист и назовите его вычислениеинтеграла.

2. Установите ширину столбца А равной11.

3. В ячейку А1 введите название Гаммафункция.

Введите значения и присвойте имена ячейкам для значений х и шага интегрирова- ния dt.

4. В ячейку С1 введите метку х= и выровняйте ее по правомукраю.

5. В ячейку D1 введите значение 1.5 и присвойте ячейке имяX.

6. В ячейку Е1 введите метку dt= и выровняйте ее по правомукраю.

7. В ячейку F1 введите значение 0.1 и присвойте ячейке имяDelT.

8. В ячейки B3:G3 введите метки 'Истина, Прям., Трап., Трап.2,, Симп.1/3 и вы- ровняйте их поцентру.

Напишите формулу сложения содержимого всех ячеек для получения пол- ного интеграла каждым методом. Вычислите ошибку каждого метода, сравнив вычисленный интеграл с правильным значением в ячейке В4.

9. Введите следующие значения в указанныеячейки.

Ячейка А4 А5	Содержание Интеграл= Ошибка=	Примечание выравнивание по правому краю выравнивание по правому краю
В4 С4	=КОРЕНЬ(ПИ())/2 =СУММ(С8:С102)	скопировать в D4:E4
С5	=(С4-$В$4)/$В$4	скопировать в D5:G5
F4	=D4+(D4-E4)/3
G4	=СУММ(G8:G102)

В столбцы А и В введите 96 значений переменной t и интегрируемого выра- жения. 10. Введите следующие значения в указанные ячейки.

10. Введите следующие значения в указанныеячейки

Ячейка Содержание Примечание

А7 t выравнивание по правомукраю

А8 О

А9 =A8+DelT скопировать вА10:А103

В7 f(x,t) выравнивание по правомукраю

11. Измените формат ячеек А8:А103 числовой, с четырьмя знакамичисловой, с четырьмя знаками на послезапятой.

12. В ячейку В8 введите формулу = EXP(-A8)*A8^(X-l) и скопируйте еев ячейкиС9:С102.Теперьвведитеформулыдляправилапрямоугольников

13. В ячейку С8 введите формулу =B8*DelT и скопируйте ее вячейки В9:В103.

Дважды проведите вычисления по правилу трапеций, первый раз с использо- ванием одинарного шага, а второй раз с использованием двойного шага интег- рирования. Второе вычисление необходимо для вычисления по формуле Ромберга в ячейке F4. Обратите внимание, что при втором вычислении по правилу тра- пеций используется каждая вторая точка, поэтому в столбце Е происходит обнуление некоторых формул, чтобы не учитывать их дважды.

14. В ячейку D8 введите формулу =DelT*(B8+B9)/2 и скопируйте ее в ячейки D9:D102.

15. В ячейку Е8 введите формулу =DelT*(B8+B10) и скопируйте ее в ячейки Е9:Е101.

16. Замените формулу в каждой второй ячейке столбца Е (Е9, Е11, Е13, ..., Е101)на0.

Введите формулы для вычисления по правилу Симпсона. Как и ранее, обну- лите каждую вторую формулу в столбце G.

17. В ячейку G8 введите формулу =DelT*(B8+4*B9+B10)/3 и скопируйте ее в ячейкиG9:G101.

18. Замените формулу в каждой второй ячейке столбца G (G9, G11,G13,

...,С101)на 0.

19. Отключите отображение линийсетки.

Теперь ваш рабочий лист должен выглядеть, как показано на рис. 8.5. Значе- ния, вычисленные по правилу прямоугольников и трапеций, практически одина- ковы. Интегрирование Ромберга уменьшает ошибку для правила трапецийпочти на 50 процентов, до значения, близкого вычисленному по правилу Симпсона. Во всех вычислениях, область интегрирования была разделена 96 равноотстоящими точками.