ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Факультет компьютерных информационных технологий и автоматики

кафедра «Горная электротехника и автоматика им. Р.М. Лейбова»

Методические указания

к выполнению лабораторных работ по курсу

"Численные методы "

(Для студентов специальности 15.03.04 «Автоматизация технологических процессов и производств»по профилю «Автоматизированное управление технологическими процессами» очной, очно-заочной и заочной форм обучения)

2016

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Методические указания

к выполнению лабораторных работ по курсу

«Численные методы»

(Для студентов специальности 15.03.04 «Автоматизация технологических процессов и производств» по профилю «Автоматизированное управление технологическими процессами» очной, очно-заочной и заочной форм обучения)

Рассмотрено

на заседании кафедры "Горная электротехника и автоматика", протокол № 4 от 15.11.2016 г.

Утверждено

на заседании учебно-издательского совета ДонНТУ

протокол № _ от ___.___.20___ г.

2016

УДК 681.3.06.

Методические указания к выполнению лабораторных работ по курсу «Численные методы» (для студентов специальности 15.03.04 «Автоматизация технологических процессов и производств» по профилю «Автоматизированное управление технологическими процессами» очной, очно-заочной и заочной форм обучения)/Ткаченко А.Е., Дубинка Е.С. - Донецк, ГОУ ВПО «ДонНТУ», 2016 - 69 с.

Представлены задачи и указания к выполнению лабораторных работ. Содержится информация по численным методам и моделям решения задач на ЭВМ.

Составители: ст.преп. Ткаченко А.Е.

ассистент Дубинка Е.С.

Ответственныйзавыпуск: проф. МареничК. Н.

Лабораторная робота № 1

Тема: Поиск корня алгебраического уравнения

1. Вводные замечания.

Задача нахождения корней нелинейных уравнений вида

F( x)=0 (1.1)

встречается в различных областях научных исследований (здесь F(x) – некоторая непрерывная функция.) Нелинейные уравнения можно разделить на два класса – алгебра и трансцендентная. Уравнениями алгебры называются уравнения, алгебраические, содержащие только (целые, рациональные, иррациональные). В частности, многочлен является целой функцией алгебры. Уравнения, другие функции (тригонометрические, показательные, логарифмические и др.), Содержащие называются трансцендентными.

Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы).

Однако встречающиеся на практике уравнение не удается решить такими простыми методами. Для их решения используются итерационные, методы, то есть методы последовательных приближении. Алгоритм нахождения корня уравнения с помощью итерационного метода состоит из двух этапов: а) отыскания приближенного значения корня или содержит его отрезка; б) уточнения приближенного значения до некоторой заданной степени точности.

Приближенное значение корня (начальное приближение) может быть найдено различными способами: из физических соображений, из решения аналогичной задачи при других исходных данных, с помощью графических методов. Если такие априорные оценки начального приближения провести не удается, то находят две близко расположенные точки а иb, в которых непрерывная функцияF(x) принимает значения разных знаков, то есть F(a)F(b)<0. В этом случае между точкамиа и b есть, по крайней мере, одна точка, в которой F(x)= 0. В качестве начального приближения Х₀ можно принять середину отрезка [а, b], то есть Х_о =(а + b)/2.

Итерационный процесс заключается в последовательном уточнении начального приближенияХ₀ . Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корняХ_0, Х_1, Х₂..., Хп. Если эти значения по возрастанию п приближаются к истинному значению корня, то говорят, что итерационный процесс сходится

1.2.Метод, деления отрезка по- долам (метод бисекции). Это один из простейших методов нахождения корней нелинейных уравнений. Он состоит в следующем. Допустим, что нам удалось найти отрезок [a , b], в котором расположено искомое значе- ние корня х = с, т. е. а < с <<b. В ка- честве начального приближения кор- ня С₀ принимаем середину этого от- резка, т. е. С₀ = (а + b)/2. Далее иссле- дуем значения функции F(x) на кон- цах отрезков [a, С₀] и [С₀ , b], т. е. в

точках a, Со, b. Тот из них, на концах которого F(x) принимает значения разных

знаков, содержит искомый корень; поэтому его принимаем в качестве нового от-

резка. Вторую половину отрезка [С₀, b], на которой знак F(x) не меняется, отбрасываем.

В качестве первой итерации корня принимаем середину нового отрезка и т. д.

Таким образом, после каждой итерации отрезок, на котором распо- ложен корень, уменьшается вдвое, т. е. после п итераций он сокращается в 2ⁿраз.

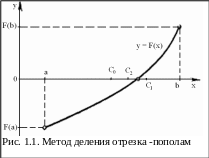
Пусть для определенности F(a) < 0,F(b)>0 (рис. 1.1.). В качестве на- чального приближения корня примем С₀ = (а + b)/2. Поскольку в рассмат- риваемом случае F(С₀)<0, то С₀ < с < b, и рассматриваем только отрезок [С₀, b]. Следующее приближение: С₁=( С₀ + b)/2. При этом отрезок [С₁, b] отбрасываем, поскольку F(С₁) >0 и F(b)> 0, т. е. С₀ <с <С₁. Аналогично находим другие приближения: С₂ = (С₀ + С₁)/2 и т.д.

Итерационный процесс продолжаем до тех пор, пока значение функции F(x) после п- й итерации не станет меньшим по модулю некоторого за- данного малого числа , т. е. \F(С_n)\ <

Можно также оценивать длину полученного отрезка: если она становится меньше допустимой погрешности, то счет прекращается.

На рис. 1.2. представлена блок-схема итерационного процесса нахождения корня уравнения (1.1) методом деления отрезка пополам. Здесь сужение отрезка производится путем замены границ а или b на текущее значение корня с. При этом значение F(a) вычисляется лишь один раз, поскольку нам нужен только знак функции F(x) на левой границе, а он в процессе итераций неменяется.

Метод деления отрезка пополам довольно медленный, однако он всегда схо- дится, т. е. при его использовании решение получается всегда, причем с заданной точностью (разумеется, в рамках разрядности ЭВМ). Требуемое обычно большее число итераций по сравнению с некоторыми другими методами не является пре-

пятствием к применению этого метода.

3. Метод хорд. Пусть мы нашли отрезок [a, b], на котором функция F(x) меняет знак. Для определенности примем F(a)>0, F(b) <0 (рис. 1.3.). В данном методе процесс итераций состоит в том, что в качестве приближений к корню уравнения (1.1) принимаются значения С₀ ,С₁ ,... точек пересечения хорды с осьюабсцисс.

Сначала находим уравнение хорды АВ:

Рис. 1.3. Метод хорд

yF(a)

F(b) F(a)

_xa

ba

Для точки пересечения ее с осью абсцисс

(х = С₀ у = 0) получим уравнение

C₀ a 

b a

F(b)F(a)

F(a)

(1.2)

Далее, сравнивая знаки величин F(a) и F(С₀) для рассматриваемого случая, приходим к выводу, что корень находится в интервале (а, С₀), так как F(a)F(С₀)<0. Отрезок [С₀,b] отбрасываем. Следующая итерация состоит в опре- делении нового приближения С₁ как точки пересечения хорды AB₁ с осью абс- цисс и т. д. Итерационный процесс продолжается до тех пор, пока значение F(С_n) не станет по модулю меньше заданного числа .

Блок-схема метода хорд аналогична приведенной на рис. 1.3. для метода де- ления отрезка пополам с той лишь разницей, что вместо вычисления приближе- ния корня по формуле С₀ = (а + b)/2 нужно использовать формулу (1.2).

Кроме того, в блок-схему необходимо ввести операторы вычисления значе-

ний F(x) на границах новых отрезков.

Как видим, алгоритмы метода деления отрезка пополам и метода хорд похо- жи, однако второй из них в ряде случаев дает более быструю сходимость итера- ционного процесса. При этом успех его применения, как и в методе деления от- резка пополам, гарантирован.

3. Метод Ньютона (метод касательных).Его отличие от предыдущего ме- тода состоит в том, что на k-й итерации вместо хорды проводится касательная к кривой у =F(x) при х = С_k и ищется точка пересечения касательной с осью абс- цисс. При этом не обязательно задавать отрезок [а, b], содержащий корень урав- нения (5.1), а достаточно лишь найти некоторое начальное приближение корня

х = С₀ (рис.1.4.).

Уравнение касательной, проведенной к кривой у =F(x) в точке M₀ с координатами C₀ и F(C₀ ), имеет вид

y - F(C₀ ) = F’(C₀ )(x - C₀ ).

Отсюда найдем следующее приближение корня C₁ как абсциссу точки пересечения касательной с осью x(у= 0):

C₁= C₀- F(C₀)/ F^/( C₀).

Рис. 1.4. Метод касательных

Аналогично могут быть найдены и следующие приближения как точки пере- сечения с осью абсцисс касательных,

проведенных в точках M₁ , М₂ и т. д. Формула для п+ 1-го приближения имеет вид

C_{n + 1}= C_n- F(C_n)/F^/(C_n). (1.3)

При этом необходимо , чтобы F^/( C_n) не равнялась нулю. Для окончания ите- рационного процесса может быть использовано или условие |F(C_n)|<, или усло- вие близости двух последовательных приближений: | C_{n + 1}- C_n | <.

Из (1.3) следует, что на каждой итерации объем вычислений в методе Нью- тона больший, чем в рассмотренных ранее методах, поскольку приходится нахо- дить значение не только функции F(x), но и ее производной. Однако скорость сходимости здесь значительно выше, чем в других методах.