Тема: Основы биомеханического контроля.

План.

1. Биомеханический контроль как элемент системы комплексного контроля в физическом воспитании.

2. Понятие о биомеханических характеристиках. Их виды.

3. Кинематические характеристики.

4. Динамические характеристики.

5. Энергетические характеристики.

1. Биомеханический контроль как элемент системы комплексного контроля в физическом воспитании.

Двигательное мастерство человека, его умение в любых условиях двигаться быстро, точно и красиво, зависит от уровня физической, технической, тактической, психологической и теоретической подготовленности. Эти пять факторов культуры движений являются ведущими и в спорте, и в физическом воспитании школьников, и при занятиях массовыми формами физкультуры. Для совершенствования двигательного мастерства и даже для сохранения его на прежнем уровне необходим контроль за каждым из названых факторов.

Объектом биомеханического контроля служит моторика человека, т.е. двигательные (физические) качества и их проявления. Это означает, что в итоге биомеханического контроля мы получаем сведения:

1) о технике двигательных действия и тактике двигательной деятельности;

2) о выносливости, силе, быстроте, ловкости и гибкости, должный уровень которых является необходимым условием высокого технико-тактического мастерства (в англоязычной литературе по физическому воспитанию принят более широкий перечень двигательных качеств, в том числе способность выполнять упражнения на равновесие, танцевальные упражнения и т.д.).

Можно сказать, ещё проще: биомеханический контроль даёт ответ на три вопроса:

1. Что делает человек?

2. Насколько хорошо он делает это?

3. Благодаря чему он это делает?

Процедура биомеханического контроля соответствует следующей схеме:

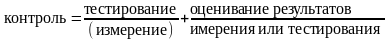
2. Понятие о биомеханических характеристиках. Их виды.

Характеристики движений человека – это те особенности (или признаки), по которым движения различаются между собой.

Когда характеристики вычисляют или измеряют – это количественные характеристики.

Когда характеристик описывают только словами (без измерений) – это качественные характеристики.

Биомеханическими характеристиками называются показатели, используемые для количественного описания и анализа двигательной деятельности. Все биомеханические характеристики делятся на кинематические, динамические и энергетические. У них разное назначение: кинематические характеризуют внешнюю картину двигательной деятельности, динамические несут информацию о причинах изменения движений, энергетические дают представление о механической производительности и экономичности.

Биомеханические характеристики описывают поступательные и вращательные движения. Поступательным называется такое движение, при котором все точки тела перемещаются по одинаковым траекториям. При вращательном движении движущиеся точки тела перемещаются по круговым траекториям, центры которых лежат на оси вращения.

Поступательное движение – движение при котором любая прямая, соединяющая какие-либо две точки тела остаётся параллельной самой себе.

3. Кинематические характеристики.

Кинематические характеристики – количественные характеристики, раскрывающие форму (рисунок) и характер движений (изменение во времени – быстрее, чаще и т.д). Они описывают движение в пространстве и во времени.

а) Пространственные характеристики (координата перемещение, траектория).

Координата точки – это пространственная мера местоположения точки относительно системы отсчета.

Перемещение точки – это пространственная мера изменения местоположения точки. Перемещение (линейное)определяют, измеряя разность координат в моменты начала и окончания движения (в одной и той же системе отсчёта расстояния):

– линейное перемещение,

 кон – нач – угловое перемещение,

угол поворота тела или сегмента; т.е. это величина и направление отрезка прямой от начального положения точки до конечного – это векторная величина.

Траектория точки – это пространственная мера движения (воображаемый след движущейся точки). Траекторию определяют, устанавливая её длину, кривизну и ориентацию в пространстве.

Длина траектории – путь.

Кривизна траектории – h = ; R – радиус окружности.

Ориентация траектории – определяют по координатам точек начального и конечного положения: и третей точки, не лежащей на одной прямой.

б) Временные характеристики.

Момент времени – это временная мера положения точки, тела системы. Момент времени определяют промежутком времени до него от начала отсчёта.

t

Моментами времени обозначают, начало и окончания движения или какой-либо его части (фазы).

Длительность (цикла) – интервал времени между одинаковыми фазами циклического движения Т = .

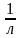Длительность движения – это его временная мера, которая измеряется разностью моментов времени окончания и начала движения:

t = tкон – tнач .

Темп движений – это временная мера повторности движений (число движений в единицу времени). Он измеряется количеством движений, повторяющихся в единицу времени (частота движений): N = .

N = 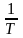Темп – величина, обратная длительности движений.

Фаза – временной элемент двигательных действий.

Ритм движений (соотношение длительностей фаз) – это временная мера соотношения частей движений. Он определяется по соотношению промежутков времени (длительность частей движений):

t ; t ; t ...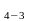

Хронограмма – графическое изображение ритма.

Неритмичные движения – это движения с отклонением от заданного ритма, либо нерациональные движения – это движения с неопределённым или неправильным ритмом.

в) Пространственно-временные характеристики.

По пространственно-временным характеристикам определяют, как изменяются положения человека во времени, как быстро человек изменяет свои положения (скорость) и движения (ускорение).

Скорость точки – это пространственно-временная мера движения (быстрота изменения положения). Скорость измеряется отношением пройденного пути ( с учётом его направления) к затраченному времени:

 

Vср = .



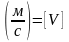V – величина векторная; она характеризует быстроту (численное значение – модуль) и направление движения.



V бывает постоянной – равномерное движение;

V изменяется – неравномерное движение.

Мгновенная скорость точки – это мера быстроты изменения положения точки в данный момент времени. Она измеряется пределом отношения длинны перемещения к его времени, когда промежуток времени стремится к нулю.

  

Vt = lim [V] =

Средняя скорость – это такая постоянная скорость, с которой точка за все заданное время прошла бы рассматриваемый путь за заданное или действительно затраченное время.

Скорость точки (линейная) в прямолинейном движении направлена по траектории, в криволинейном – по касательной к траектории в каждой рассматриваемой точке.

Скорость тела определяют по скоростям его точек.

При поступательном движении линейные скорости всех точек тела одинаковы по величине и направлению.

При вращательном движении, чем больше расстояние точки тела от оси вращения (т.е. больше радиус), тем больше её линейная скорость.

В твёрдом теле:

Угловая скорость – отношение линейной скорости каждой точки к её радиусу. Угловая скорость (W) для всех точек тела одинакова:

[W] = .

Линейная скорость любой точки вращающегося тела равна его угловой скорости, умноженной на радиус вращения этой точки (её расстояние до оси вращения):

V = Wr W = [W] .

Скорость системы тел, изменяющей свою конфигурацию. Нельзя определить таким же способом, как у твёрдого тела.

В этом случае можно определить линейную скорость общего центра тяжести системы.

Часто определяют линейные скорости определенных точек звеньев тела (проекций оси суставов на поверхность тела).

Ускорение точки – это пространственно-временная мера изменения движения (быстрота изменения скорости по величине и направлению). Ускорение измеряется отношением изменения скорости к затраченному на него времени:

 

аt = lim ; [а] = .

Ускорение – величина векторная.

Ускорение точки положительное – если величина её скорости становится больше (без изменения направления):

 

а сонапр. с V.

Ускорение точки отрицательное – величина скорости становится меньше (без изменения её направления). Отрицательно ускорение направлено в сторону, противоположную скорости.

Нормальное ускорение имеет место, когда величина скорости остаётся прежней, но изменяется её направление (это ускорение перпендикулярное направлению скорости).

В криволинейном движении точки её положительные и отрицательные ускорения направлены по касательной к траектории (тангенциально), а нормальное (радиальное) – вдоль радиуса кривизны (центростремительно – к центру; центробежное – от центра кривизны траектории).

Линейное ускорение – в поступательном движении.

Угловое ускорение – во вращательном движении.

Угловое ускорение – отношение линейного ускорения каждой точки вращающегося тела к её радиусу.

Е = [E] =

E = [E] =

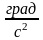
Линейное ускорение любой точки вращающегося тела равно его угловому ускорению, умноженному на радиус вращения этой точки:

а = Еr

В биокинематических цепях тела человека движение может передаваться от звена к звену. Таким образом, движение, например, кисти при броске мяча может быть результатом движения ног и туловища, а так же движений в суставах руки.

Движение кисти в этом случае как бы составляется из движений и других звеньев.

Такое движение в биомеханике называется СОСТАВНЫМ.

Составное движение образуется из нескольких составляющих движений в сочленениях биокинематической цепи.

В механике складываются поступательные и вращательные движения.

Движение хоккеиста и шайбы. Сложение двух поступательных движений.

Vтел + Vгруз = Vрезульт (относительно земли)

Одинаково направленные – суммируются

Разнонаправленные – вычитаются

Сложение поступательных и вращательных движений.

В зависимости от изменения направления скоростей и их сложения, движения звеньев тела человека могут быть 1) возвратно-вращательные, 2) возвратно-поступательные, 3) круговые.

Возвратно-вращательные движения напоминают движения маятника (колебательные движения) вокруг оси, расположенной поперёк биокинематической цепи (сгибание-разгибание) или продольно (супинация-пронация).

Возвратно-поступательное возникает при определённом согласовании вращательных движений в различных суставах биокинематической цепи, позволяющее конечным звеньям двигаться поступательно (кисть боксёра при вращательных движениях в плечевом и локтевом суставах; туловище бегуна при отталкивании ногой; робота пилой, напильником).

Круговое движение возможно в шаровидных суставах, когда продольная ось звена описывает коническую поверхность. Только оно выполняется без обязательных возвратных движений.