3.31. Исследование поведения функций и построение графиков

Определение 3.5. Функция на интервале (a; b) монотонно

не убывает, если

не возрастает, если

строго возрастает, если

строго убывает, если

где

Теорема 3.8. (необходимое и достаточное условие монотонности функции на интервале).

Для того, чтобы функция непрерывная на [a; b] и дифференцируемая на (a; b) не убывала (не возрастала) на (a; b), необходимо и достаточно, чтобы ( ) для всех

Доказательство

Необходимость. Пусть не убывает на (a; b), т.е. Пусть Тогда и .

Следовательно, (по теореме о знаке предела), т.е. .

Необходимость доказана.

Достаточность. Пусть непрерывна на [a; b]. Тогда по теореме Лагранжа для всех выполняется

где по условию теоремы. Следовательно, и не убывает по определению, что и требовалось доказать.

Замечание (геометрический смысл теоремы)

Если на интервале (a; b) функция возрастает, то касательная к кривой в каждой точке на этом отрезке образует с осью Ox острый угол или – в отдельных точках – горизонтальна; тангенс этого угла не отрицателен: (рис 3.17). Если функция убывает на интервале (a, b), то угол наклона касательной – тупой (или – в отдельных точках – касательная горизонтальна); тангенс этого угла не положителен (рис. 3.18). Теорема позволяет судить о возрастании или убывании функции по знаку ее производной.

Рис. 3.17 Рис. 3.18

Следствие. Для того, чтобы ( ) на (a, b) необходимо и достаточно, чтобы для всех

Пример. Найти интервалы возрастания и убывания функции

Решение. Функция определена для всех

З нак

поведение y

Следовательно, при возрастает; при убывает; при возрастает.

3.32. Экстремум функции

Пусть функция непрерывна на некотором промежутке, включающем точку .

Определение 3.6. Точка называется точкой строгого локального максимума (минимума) функции , если для всех x из некоторой - окрестностей точки выполняется неравенство при .

(рис. 3.19).

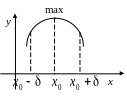
Рис. 3.19

Локальный максимум (max) или локальный минимум (min) объединяются общим названием локальный экстремум.

Из определения следует, что понятие экстремума носит локальный характер в том смысле, что неравенство может и не выполняться для всех значений x в области определения функции, а должно выполняться лишь в некоторой окрестности точки .

Очевидно, функция может иметь несколько локальных максимумов и несколько локальных минимумов, причем может так случиться, что иной локальный максимум окажется меньше какого-то локального минимума. (рис. 3.20)

Рис. 3.20.

Теорема 3.9. (необходимое условие локального экстремума).

Если функция имеет в точке локальный экстремум и дифференцируема в этой точке, то .

Определение 3.7. Точки, в которых производная функции равна нулю, называют стационарными точками этой функции.

Из теоремы 3.9 следует, что дифференцируемая функция может достигать экстремума только в своих стационарных точках. Из рис. 3.21 видно, что в точках, где производные бесконечны или не существуют, функции также могут иметь экстремум.

Рис. 3.21.

Но могут возникнуть случаи, когда эти условия относительно производной выполняются, а экстремума функции не существует (Рис. 3.22)

Рис. 3.22.

Итак, необходимое условие экстремума в точке :

Определение 3.8. Точки, в которых производная функции равна нулю, бесконечна или не существует, называются критическими точками функции или точками, подозрительными на экстремум.

Теорема 3.10. (Достаточные условия существования экстремума).

Пусть функция непрерывна на некотором интервале, содержащем критическую точку , и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки ). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то при функция имеет максимум. Если же при переходе через точку слева направо производная меняет знак с минуса на плюс, то функция имеет в этой точке минимум.

Пример

Найти экстремумы функции

Решение

Найдем производную .

Точки, подозрительные на экстремум, Отметим, что в точке x=0 функция терпит разрыв и потому не может иметь экстремум.

Найдем знак производной в окрестностях критических точек.

x		-1		0		1
	+	0	-		-	0	+
y		max		разрыв		min

Итак, максимум минимум

Теорема 3.11. (достаточный признак экстремума через вторую производную).

Пусть тогда при функция имеет максимум, если и минимум, если

Пример

Найти экстремумы функции через вторую производную.

Решение

Найдем Значения в критических точках Значит, максимум минимум