2.1 Күй функциясы. Күйлердің суперпазитция принципі

Де Бройлдің микробөлшектердің корпускулалық толқындық табиғаты туралы гипотезасы дұрыс екендігі тәжірибемен нақтыланғаннан кейін микробөлшектер қозғалысы үшін классикалық механикадағы әдістер жарамайтындығы белгілі болды. Сондықтан микробөлшектердің кұйін сипаттайтын жаңа құрал қажет болды Ондай құрал ретінде жаңа түсінік – толқындық функция немесе күй функциясы деп аталатын Ψ пси функция енгізілді. Күй функциясы әрбір бөлшекпен байланысты болатын толқындық өрістің математикалық сипаты болып табылады. Толқындық функция микробөлшектердің параметріне тәуелді болады және микробөлшектердің физикалық шарттарына да тәуелді болады. Ψ толқындық функция микробөлшектердің механикалық күйін толқындық сипаттай алады және белгілі бір жүйеде болуының ықтималдылығымен анықталады. Айталық Ψ(x, y, z, t) берілсін онда бөлшектің t уақыт мезетінде координаттары x, y, z болатын dV элементар көлемде болу ықтималдылығы келесі өрнекпен анықталады. (1) Бұл өрнектен: - микробөлшектің орнын анықтайтын ықтималдылық тығыздығы деп аталады. Күй функциясы (Ψ) комплексті шама яғни оның модульінің квадраты. (2) Мұндағы: комплекс түйіндес функция екенін көрсетеді. Комплекстік функция әрқашанда былай жазылады. (3) Мұндағы: функция модульі. Ал —фразалық жиын деп аталады.Сонымен пси күй функциясы жеке өзінің физикалық мағынасы жоқ, бірақ оның квадраты микробөлшектің кеңістіктің қандайда бір V көлемде болу ықтималдығын береді. Бірінші бөлшекті интегралдау арқылы. (4) Ықтималдылықтың жиынтығын табуға болады, бұл күйлердің суперпазитсия принципі деп аталады. Егер (4) интегралды бүкіл кеңістік бойынша интегралдасақ. (5) . (5) өрнек күй функциясының нормалау шарты деп аталады. Ψ – функция теориялық жолмен анықталғанда (5) интеграл 1-ге емес қандайда бір n деген санға тең болып қалады. Яғни Ψ функция нормаланбаған болып шығады. Сондықтан мұндай жағдайда Ψ функция нормалау үшін Ψ функция ге көбейту қажет болады. Сонымен Ψ функция микробөлшектің күйін сипаттау үшін келесідей шарттарды қанағаттандыру керек.

1. Ψ функция 1 мәнді болуы керек

2. Ψ функция үздіксіз болуы керек

3. Ψ функция квадрат – интегралдық болуы шарт.

Классикалық механикалық физиканың басқа бөлімдеріндегі сияқты суперпазиция принципі орындалады. Ол былайша тұжырымдалады : Берілген шарттарды қанағаттандыратын толқындық функциясы арқылы сипатталатын әртүрлі күйдегі бөлшектер берілген жағдайда келесі сызықтық комбинатциямен сипатталатын бөлшектің күйі де бола алады. (6) Бұл теңдеу Классикалық механикадағы суперпазитция принципі.Мұндағы: = комплекстік сандар. Классикалық механикадағы суперпазитция принциі былайша толығырақ айтуға болады: Берілген шарттағы бөлшектің Ψ функциясы мен сипатталатын болса яғни 6 шы өрнек орындалатын жағдайда бөлшектің ықтималдылығы күйде болуы. күйде болу ықтималдылығына тең болады. Сонымен толқындық функцияны қосу микробөлшектер әлеміндегі күйлердің суперпазитциясының ерекшелігі болып табылады, яғни толқындық функция микробөлшектердің күйін сипаттайтын математикалық құралдың негізі болып табылады.

2.2

Классикалық механикадағы макро бөлшектердің (материалдық нүктенің) кез-келген уақыт мезетіндегі механикалық күйін сипаттайтын теңдеу болып табылады. Ал кванттық механикада (7) теғдеуге пара-пар теңдеу, яғни микро бөлшектің күйңн сипаттайтын толқындық функция түрінде жазылады. ,t) (8) Классикалық механикадағы негізгі мәселе материалдық нүктенің кез-келген уақыт мезетіндегі орны мен жылдамдығы анықтау болатын. Бұл мәселе классикалық механиканың негізгі теңдеуі-Ньютонның екінші заңымен іске асады. Кванттық механикада берілген уақыт мезетіндегі күштік өрістегі орнын анықтау. Кванттық механикадағы негізгі теңдеу-Шредингер теңдеуінің көмегімен іске асады. Щредингер теңдеуінің жалпы түрі мына түрде жазылады: 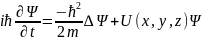(9) Бұл дербес туындысы бар дифференциялдық теңдеу, Мұндағы: і-жорамал бірлік, Лаплас операторы, m бөлшек массасы, толқындық функция, бөлшектің сыртқы күштікөрістегі потенциялдық энергия. Нақты есептерде Потенциялдық энергияның координатасымен уақытқа тәуелділігінің бірнеше жағдайы болуы мүмкін. функциясы берілген жағдайда (9) Щредингер теңдеулерінің жалпы шешімін табуға болады. Жалпы шешім қандай да бір координатамен уақытқа тәуелді еркін функциядан тұрады. Бұл функцияны бастапқы және шекаралық шарттардың көмегімен анықтайды. Бастапқыт шарт (t=0) кезде (10) . Шекаралық шартты анықтауда толқындық функцияның мәндеріне қандай да бір кеңістіктің шекарасындағы немесе шексіздіктегі мәндерін береді. Бастапқы және шекаралық шарттардың және нормалау шартының жиыны толқындық функцияның, яғни Щредингер теңдеуінің дербес шешімдерін береді. Ψ-функциясы анықталған жағдайда кез-келген уақыт мезетіндегі күйін сипаттауға болады. Бұл кванттық механикадағы себептілік принціпінің негізін қалайды. Ол былайша тұжырымдалады: Ψ-функцияның бір мәнді динамикалық заңдылығы болған жағдайда микробөлшектің статистикалық заңдылығын анықтауға болады. Сонымен кванттық механиканыңнегізгі теңдеуі сызықтың біртекті және дербес туындылардан тұратын дифференциялдық теңдеу болып табылады. Стационар потенциялдық өрістегі, яғни потенциялдық энергиясы уақытқа тәуелді болмайтын өрістегі бөлшектің қозғалысын қарастыру теориялық және практикалық маңызға ие. Ол үшін Щредингер теңдеуін 2 тәуелсіз функцияға жіктейді. (10) Осы өрнекті Щредингер теңдеуіне қояиық. 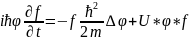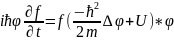(11) , (12)

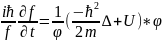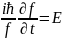(12) теңдеудің екі жағын да ке бөлейік (12*) (12*)-өрнектің сол жағымен оң жағы әр түрлі айнымалыларға тәуелді функция. Бұл теңдеудің сол жағындағы (13*) , (13**) Сонымен толқындық функцияның уақытқа (13) және координатаға (14) тәуелді екі өз-ара тәуелсіз 2 теңдеулерге бөлдік. (13)-теңдеудің жалпы шешімі математикадан белгілі. (14) . Бұл теңдеу Щредингердің стационар теңдеуі деп аталады. Әдетте оны мына түрде жазады:

.Әдетте оны мына түрде жазады: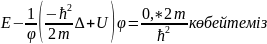

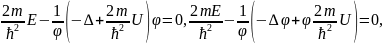
(16)