2.3. Ықтималдық ағынының тығыздығы.

Микробөлшектің қозғалысы кеңістікте 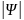² ықтималдылық тығыздығы бойынша таралуымен сәйкес келеді. Яғни бөлшектің кеңістіктегі қозғалысы ықтималдылықтар ағынының тығыздығы деп аталатын арнайы шаманың көмегімен сипатталады. Бұл шама кванттық механиканың негізгі теңдеуіне сүйене отырып алынады: 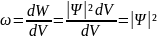, 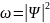(18) Бұл шаманың уақытқа тәуелді өзгеруін анықтайық: 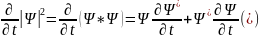Шредингер теңдеуінен:

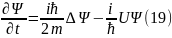
Дәл осы сияқты комплексті түйіндеудің операторын жазсақ: , (19) және (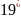 ) өрнекті (*) өрнекке апарып қойсақ:

Сонда:

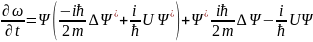
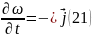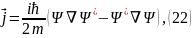
Бұдан: , (20) теңдеу былай жазылады: , Мұндағы: ықшамдықтар ағыны тығыздығының векторы.

2.4

Ықтималдықтардың сақталуын бөлшектер санының сақталуымен түсіндіруге болады, ол үшін кеңістікте бір біріне тәуелсіз бірдей кванттық күйде болатын бірдей N микробөлшектер бар деп қарастырайық. Бұл бөлшектердің барлығы бір ғана толқындық функциямен сипатталсын. Егер N>>1 болса онда кеңістіктің әрбір нүктесіндегі бөлшектер тығыздығыа тең болады. Ал - Интегралы кеңістіктің, V көлеміндегі бөлшектер санын анықтайды. Олай болса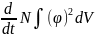 туындысы V көлемдегі бөлшектер санының бірлік уақыт ішіндегі өзгеруін сипаттайды.

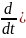, (23) Сонымен (23*), (23*) өрнек кванттық механикадағы бөлшектер санының сақталу заңы деп аталады. ОЛ былайша тұжырымдалады. Кеңістіктің қандайда бір V көлеміндегі бөлшектер ес түссіз жоғалмайды немесе жоқтан бар болмайды, ол тек басқа аймақтан енуі мүмкін немесе басқа аймаққа шығуы мүмкін.

2,5

Шредингер теңдеуін еркін бөлшектер үшін қарастырайық. Микробөлшектер әлемінде сыртқы әлем болмаған жағдайдағы потенциалдық энергиясы (U=0)-ге тең болған жағдайдағы бөлшек еркін бөлшек деп қарастырылады. Бұл стационар өрістің бір жағдайы яғни бөлшектің энергиясы сақталады. Сондықтан Шредингердің стационар өріс үшін (14)-ші теңдеуге көшуге болады. Еркін бөлшек үшін бұл теңдеуді мына түрде жазады:

Мұндағы, ,

*

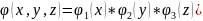
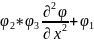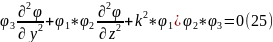
(25)-ші теңдеуді

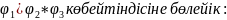
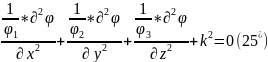
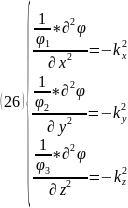
(26)-ші теңдеулер жүйесінен көрініп тұрғандай бір типті 3 теңдеу алдық.

Сондықтан, тек бір теңдеуді шешу жеткілікті.

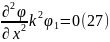. Бұл теңдеу 2-ші реттік дифференциалдық теңдеу.

Бұл теңдеу математикада толық шешілген теңдеу болып табылады және оның дербестік шешімі мына түрде жазылады:

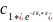
Яғни, жалпы жағдайда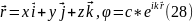

уақытқа тәуелсіз болатын тұрақты шаманы енгізейік, ондай шамаға импульс векторын жатқызуға болады.

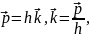сонда

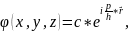
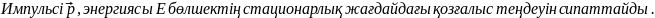
Егер уақытқа тәуелді болған жағдайда бұл теңдеуді былайша жазады.

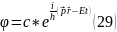
Бұл теңдеу жазық монохроматтың теңдеуі болып табылады және Дебройль теңдеуімен сәйкес келеді.

3.2

(1) және (2) теңдеулерден көрініп тұрғандай күй функциясының көмегімен бөлшектің кеңістіктегі орнын бір мәнді анықтау әрқашан мүмкін бола бермейді. Мысалы, еркін бөлшектің белгілі-бір импульсі кезінде оның координатасы кез-келген мәнге ие болуы мүмкін. Сондықтан, бөлшектің координатасы мен импульсі мейлінше аз интервалда жататын күйін сипаттайтын толқындық функцияны қарастырайық. Бір өлшемді қозғалыс кезінде импульсы P, энергиясы E еркін бөлшектің толқындық функциясы мына түрде жазылады: 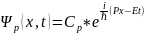(3) Импульсы 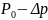және 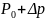интервалында үздіксіз өзгеретін функциялардың жиынтығын алайық. Мұндай сызықты комбинация келесі интеграл түрде жазылады: 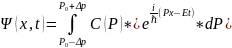(4) Бұл теңдеу толқындық топ немесе толқындық пакет деп аталады.

3.3

Толқындық пакетті жуықтап есептеу арқылы, толқындық пакеттің жекеленген құрауыштарының интерференциясы салдарынан кеңістіктің 𝛥x аймағында шоғырлануы мына өрнекпен анықталады: Яғни, толқындық пакет бір орында тұра алмайды, ох осі бойымен 𝛥х аралықта пакеттің центрі бір қалыпты қозғала алады. Пакеттің шекарасын мына өрнекпен анықтайды: 𝛥x𝛥p≥2πħ (5). (5)-өрнек-Гизенбергтің координатасы мен импульсі үшін анықталмағандықтар арақатынасы деп аталады. Бұл өрнекті үш өлшемді қозғалыс үшін былайша жазады:𝛥x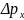 ≥2πħ

𝛥y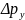 ≥2πħ (5*)

𝛥z ≥2πħ

Бұл өрнекті 1927 жылы Гизенберг қорытып алды. Бұл өрнек кванттық механикада қорытындылар жасауға маңызды рөлге ие. Гизенбергтің анықталмағандықтар арақатынасы физикалық мағынасы төмендегіше: Микробөлшектің белгілі бір траектория бойымен қозғалысы кезіндегі берілген уақыт мезетіндегі оның координатасы мен импульсін дәл анықтау мүмкін емес. Себебі, микробөлшектің берілген уақыт мезетіндегі координатасы мен импульсін қатар анықтау кезінде жіберілетін қателік 2πħ шамасынан аз болмайды.

3.4

Микробөлшектер әлемін зерттеу барысында физикалық шамаларды өлшеу деген түсінікті қайта қарауға тура келеді. Микробөлшектің координатасын өлшеудің физикалық негізіне тоқталайық.Микробөлшектің координатасын анықтау үшін, оның оның еркін қозғалысын шектеуге тура келеді. Ол өз кезегінде микробөлшектің импульсі туралы мәліметке өзгеріс енгізеді. Яғни координатасы дәл анықталған . Микробөлшектің импульсі анықталмаған болады. Дәл осы сияқты мәселе микробөлшектің импульсін анықтаудада туындайды. Яғни , толқындық қасиетке ие. Микробөлшектің координатасы мен импульсін бір мезгілде дәл анықтауға болмайды. Бұны былайша түсіндіруге болады. Бөлшектің физикалық күйін сипаттайтын шамаларды өлшегенде, бөлшекпен өлшеу құралының бір-біріне әсері болатындығын естен шығармау қажет. Яғни, бөлшек, бөлшек құралына әсер еткенде , өлшеу құралыда бөлшекке әсер етіп, оның бастапқы күйін өзгертіп жібереді. Макрожүйеде, яғни классикалық физикада өлшеу құралының макрожүйеге елеусіз аз болғандықтан ескерілмейтін, ал микроәлемде ол әсерді ескермеуге болмайды.