1.6. Частотный критерий устойчивости Найквиста
Иногда в практике возникает необходимость в анализе устойчивости замкнутой САУ по характеристикам разомкнутой её части. Критерий Найквиста позволяет определить устойчивость замкнутой системы по виду АФЧХ разомкнутой системы.
|
|
Для доказательства критерия Найквиста введём вспомогательную передаточную функцию
,
-
передаточная
функция системы в разомкнутом состоянии;
)
-
собственный оператор замкнутой системы;
-
собственный оператор системы в разомкнутом
состоянии.
Как
правило, порядок оператора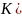
)
меньше
порядка собственного
,поэтому
порядки собственного оператора замкнутой
системы и системы в разомкнутом состоянии
совпадают.
Переходя в частотную область (s=j ), получим:
-
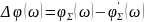
корни уравнения
-
корни характеристического уравнения
.
При анализе устойчивости замкнутой системы могут быть 2 случая:
разомкнутая система устойчива,
разомкнутая система неустойчива.
Рассмотрим
случай, когда разомкнутая система
устойчива. Будем изменять частоту от
-
до +
и
изобразим получившуюся амплитудно-фазовую
частотную характеристику
на
комплексной плоскости (рис. 1.8,а).
Рассмотрим результирующий угол поворота
вектора
при
изменении частоты от -
до +
.
Этот угол представляет собой изменение
.
Числитель в выражении
представляет
собой характеристический комплекс
замкнутой системы. Для того чтобы система
была устойчивой в замкнутом состоянии
необходимо изменение аргумента
в
диапазоне частот
равное
,
где
-
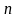степень характеристического полинома.
При изменении частоты от -
до+
аргумент
изменится на величину
.
Рис.
1.8. Годографы вспомогательной частотной
передаточной функции
(а); АФЧХ разомкнутой системы (б).
Знаменатель
в выражении (1.8) представляет собой
характеристический комплекс разомкнутой
системы той же степени n.
Так как мы рассматриваем случай устойчивой
разомкнутой системы, то результирующий
угол поворота вектора
при
изменении частоты от -
до+
будет
равен
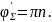
Отсюда
следует, что в рассмотренном случае
результирующий угол поворота вектора
будет
равен нулю:
.
Это означает, что для устойчивой в
замкнутом состоянии системы годограф
вектора
не
должен охватывать начала координат
(рис. 1.8,а).
Частотная
функция
разомкнутой системы отличается от
вспомогательной функции
на
единицу. Поэтому можно строить
амплитудно-фазовую частотную характеристику
разомкнутой системы и по ее виду
анализировать устойчивость замкнутой
САУ. В этом случае амплитудно-фазовая
частотная характеристика разомкнутой
системы не должна охватывать точку с
координатами (-1;
j0)
(рис.
1.8,б).
Из доказанного следует формулировка критерия Найквиста:
Для устойчивости замкнутой САУ, полученной замыканием устойчивой разомкнутой системы, необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала точку с координатами (-1; j0).
На рис. 6.9 приведены примеры частотных характеристик разомкнутых систем, соответствующих устойчивым и неустойчивым замкнутым системам.
Вследствие
симметрии ветвей (относительно
действительной оси) обычно строят ветви
АФЧХ, соответствующие аналитическому
решению в диапазону частот
.
Второй случай - разомкнутая система неустойчива.
Наличие
неустойчивости системы в разомкнутом
состоянии не означает, что система будет
неустойчивой в замкнутом состоянии.
Она может быть как устойчивой, так и
неустойчивой. Однако формулировка
критерия устойчивости Найквиста при
этом несколько меняется. Пусть знаменатель
передаточной функции разомкнутой
системы
степени
n
содержит k
корней с положительной вещественной
частью.
а) и б) – устойчивым замкнутым системам; в) – системе на границе устойчивости;
г) – неустойчивой замкнутой системе.
Рис. 1.9. АФЧХ разомкнутой системы, соответствующие
Тогда
при изменении частоты от -
до+
аргумент
повернётся
на угол
.
Для
устойчивой замкнутой системы при
изменении частоты от -
до +
.
Следовательно, аргумент
будет равен
.
Это означает, что вектор годографа охватывает на комплексной плоскости начало координат в положительном направлении столько раз, сколько корней характеристического уравнения системы в разомкнутом состоянии находится в правой полуплоскости.
Итак,
для устойчивости замкнутой системы,
полученной замыканием неустойчивой
разомкнутой системы, необходимо и
достаточно, чтобы при изменении частоты
от -
до +
АФЧХ разомкнутой системы охватывала в
положительном направлении точку с
координатами (-1;
j0)
столько раз, сколько положительных
корней имеется в характеристическом
уравнении, соответствующем разомкнутой
системы (рис. 1.10). При изменении
от 0до
+
годограф
АФЧХ 2-го рода должен охватывать точку
(-1;
j0)
раз.
Рис. 1.10. Вид годографа неустойчивой разомкнутой системы для случая, когда замкнутая система устойчива (в характеристическом уравнении разомкнутой САУ – два корня с положительной вещественной частью).
Таким образом, при использовании критерия Найквиста, вообще говоря, необходимо убедиться в том, имеются ли в знаменателе передаточной функции разомкнутой системы корни, лежащие в правой полуплоскости (корни с положительной вещественной частью), и сколько имеется таких корней.
Следует заметить, что в практике желательно избегать второго случая, т.е. необходимо использовать только устойчивые в разомкнутом состоянии системы.
Это объясняется тем, что, если система в разомкнутом состоянии неустойчива, то при её замыкании и имеющихся в реальной системе нелинейностях может на некоторых режимах произойти нарушение устойчивой работы и возникновение автоколебаний.