Министерство образования и науки Российской Федерации
Федеральное государственное автономное
Образовательное учреждение высшего образования
«Самарский национальный исследовательский университет
имени академика С.П. Королёва»
Институт эксплуатации авиационной техники
Кафедра автоматических систем энергетических установок
Отчет по лабораторной работе
«Устойчивость систем автоматического регулирования»
.
Выполнил: студент группы 3404
Мальцев А.
Руководитель:
Профессор кафедры АЭУ Санчугов В.И.
САМАРА 2016
1 УСТОЙЧИВОСТЬ ДВИЖЕНИЯ МЕХАНИЧЕСКИХ
УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
1.1 Понятие об устойчивости движения
Одной
из основных задач теории автоматического
управления является изучения динамических
процессов изменения режимов работы
механических устройств, как объектов
управления. Системы автоматического
управления должны при нормальных
условиях эксплуатации объектов
поддерживать заданные режимы их работы.
При этом нормально функционирующая
система должна уменьшить появившиеся
рассогласование между заданным и
фактическим режимами работы. Однако,
на практике может получиться так, что
под действием возмущений это рассогласование
увеличивается, что приводит к нарушениям
заданного режима работы. В качестве
примера на рис. 1.1 представлены переходные
процессы изменения регулируемого
(выходного) параметра
системы после появившегося рассогласования
.
а – в устойчивой системе; б – в неустойчивой системе;
в – в системе, находящейся на границе устойчивости
Рис. 1.1. Переходные процессы изменения регулируемого параметра .
после действия возмущения
При этом если начальное рассогласование системы (рис. 1.1,а) стремиться к нулю, и система возвращается к исходному заданному положению (или к первоначальному заданному режиму движения), такую систему называют устойчивой.
Если начальное рассогласование системы увеличивается – систему называют неустойчивой (рис. 1.1,б) и наконец, если система после первоначального возмущения совершает незатухающие колебания говорят, что система находится на границе устойчивости.
Поэтому понятие устойчивости формулируется следующим образом. Устойчивость движения устройств, машин и механизмов это способность сохранить под действием собственных внутренних сил заданное положение или режим движения после действия управляющего воздействия или возмущения.
1.2 Условия устойчивости движения
В
общем случае движения объекта управления,
которое оценивается изменением
регулируемого параметра
описывается дифференциальным уравнением
при входном воздействии
:
1.1
а – в устойчивой системе; б – в неустойчивой системе;
в – в системе, находящейся на границе устойчивости
Рис. 6.1. Переходные процессы изменения регулируемого параметра .
после действия возмущения
Как
это принято в автоматике, уравнение
(1.1) составляется таким образом, что в
левой части уравнения представлено
изменение выходного параметра системы
и все его производные со своими
коэффициентами
.
Эти коэффициента отражают внутренние
(собственные) свойства управляемого
объекта и определяются его схемами,
устройством, размерами и др. параметрами
конструкции.
Коэффициенты
.отражают
свойства действующих возмущений и
управляющих воздействий.
Определить движение объекта управления – значит решить дифференциальное уравнение (1.1) относительно регулируемого параметра . Решение уравнения (1.1) представляет собой сумму общего и частного решений:
(1.2)
Общее
решение
описывает решение уравнения (1.1) при
правой части, равной нулю. Такое уравнение
общепринято называть однородным. Решение
однородного уравнения описывает движение
системы, которое происходит под действием
соответствующих внутренних свойств
при отсутствии возмущений и каких либо
управляющих воздействий.
Частное
решение уравнения (1.1)
определяет движение системы, происходящее
под действием возмущений и управляющих
воздействий. При этом движение системы
не может прекратиться и всегда происходит
с параметрами, определяемыми этими
возмущениями и воздействиями.
Именно потому для определения устойчивости движения необходимо решать не полное уравнение (1.1), а только однородное уравнение, в котором правая часть равна нулю:
(1.3)
Решение такого уравнения записывается в виде:
(1.4)
где:
- постоянные интегрирования, определяемые
начальными условиями решения;
(1.5)
Уравнение
(1.4) показывает, что движение системы
является суммой составляющих
и определяется величиной корней
характеристического уравнения (1.5).
Рассмотрим вид составляющих движения системы от вида корней, представленный на рис. 1.2.
Корни могут быть вещественными, комплексными и чисто мнимыми.
1.
Вещественный корень.
Если он отрицательный (
,
где
- действительное число, большее 0), то
слагаемое, определяемое этим корнем в
(1.2), будет представлять собой экспоненту
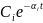(рис.
1.2,а). Очевидно, что при
составляющая движения будет затухать.
При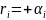
получится расходящийся процесс
(рис. 1.2,б).
2.
Комплексные корни.
Комплексные корни - всегда попарно
сопряженные. При отрицательной
вещественной части два корня, например
r,
и ri+1,
будут иметь вид.
.
В этом случае слагаемые, определяемые
этими корнями в (1.3), могут быть представлены
в виде:
,
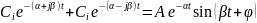где
и
- новые постоянные интегрирования.
Нетрудно
видеть, что в этом случае получаются
затухающие колебания, причем мнимая
часть корня
представляет собой круговую частоту
затухающих колебаний, а
-
показатель затухания, определяющий
затухание огибающей к кривой переходного
процесса (рис. 1.2,в).
При положительной вещественной части корня
колебания будут расходящимися (рис. 6.3,г):
.
3.
Чисто мнимые корни.
В этом случае
,
.
Слагаемое, определяемое этими корнями в (6.3), будет представлять собой незатухающие колебания с постоянной амплитудой:
.
Такой процесс изображен на рис. 1.2,д.
а) случай отрицательного вещественного корня; б) случай положительного вещественного корня; в) случай комплексно-сопряженных корней с отрицательной вещественной частью; г) случай комплексно-сопряжённых корней с положительной вещественной частью; д) случай чисто мнимых корней
Рис. 1.2. Изображение условий устойчивости в плоскости корней