6. Общие методические указания и рекомендации по выполнению контрольных работ

Предлагаемые контрольные работы содержат задачи по основным разделам физики. В основу каждой задачи положено то или иное частное проявление одного или нескольких фундаментальных законов природы и их следствий. Перед решением задач следует тщательно проработать теорию вопроса, поскольку без знаний теории невозможно успешное решение и анализ даже сравнительно легких задач.

Таким образом, решение и анализ задач позволяют понять основные законы физики, создают представление об их характерных особенностях и границах применения.

Умение решать задачи является основным критерием оценки знаний студента.

Решение большинства задач, в которых требуется выполнить расчет конкретных физических величин можно разделить на следующие этапы:

1. Анализ исходных данных, графическая интерпретация рассматриваемого процесса;

2. Установить, какие физические закономерности лежат в основе рассматриваемого процесса, составить уравнения, связывающие физические величины, характеризующие рассматриваемое явление количественно;

3. Совместное решение уравнений и анализ полученных результатов.

7. Примеры решения задач

Задача 1. Определить угол, под которым тело брошено к горизонту, если максимальная высота подъема тела равна 1/4 дальности его полета (рисунок 2). Сопротивлением воздуха пренебречь.

Решение:

Разложим скорость u₀ на составляющие

u_0х = u₀ cos a и u_0у = u₀ sin a,

где u_0х , u_0у - начальные скорости движения вдоль осей х, у соответственно (рисунок 2).

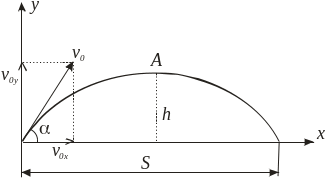
Рисунок 2 – Траектория движения тела

Высота h подъема теларавна

, (1)

где – время подъема, t – полное время полета.

Вертикальная скорость u_y = u_0y – gt₁ = 0 в точке А, откуда . Подставив в выражение (1) время подъема t₁, получим

(2)

Дальность полета

(3)

Из условия h = имеем: , откуда , или и .

Ответ: a = 45⁰.

Задача 2. Тело массой m₁ = 1 кг вращается на тонком стержне в вертикальной плоскости. Частота вращения равна n = 2 с^-1, длина стержня R = 12,5 см. Определить силу натяжения стержня: 1) в верхней точке; 2) в нижней точке.

Решение:

1 )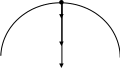

T₁

P

ma_ц

На тело в верхней точке действует сила тяжести Р = mg и сила натяжения Т стержня. В результате действия двух сил тело движется по окружности, т.е. с центро­стремительным ускорением

a_ц = w²R, (1)

где w - угловая скорость; R – радиус траектории.

Учитывая, что w = 2p n , можем записать

a_ц = 4p²n²R. (2)

Направление сил Т₁ и Р совпадает с вектором а_ц, поэтому второй закон Ньютона запишем в скалярной форме:

T₁ + mg = ma_ц (3)

или с учётом (2)

T₁ + mg = 4mp²n²R, (4)

откуда

T₁=m(4p²n²R - g) (5)

Вычислим по формуле (5) искомую силу натяжения стержня в верхней точке траектории: Т₁ = 1× (4 × 3,14² × 2² × 0,125 – 9,81) Н = 9,91 Н.

2 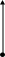) Т₂

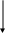ma_ц

P

В нижней точке траектории на тело действуют те же силы Р = mg и Т₂. Однако сила Р в данном случае направлена противоположно вектору а_ц.. В связи с этим второй закон Ньютона имеет вид:

T₂ – mg = 4mp²n²R ,

откуда T₂ = m(g+ 4p²n²R).

После подстановки имеем:

Т₂ = 1× (9,81 + 4 × 3,14² × 2² × 0,125) Н = 29,53 Н.

Ответ: T₁=9,91 Н; Т₂ = 29,53 Н.

Задача 3. На однородный сплошной цилиндрический барабан массой M = 7,5 кг и радиусом R = 20 см намотана легкая нить, к концу которой прикреплен груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом составляла h = 2,3 м. Определить время t опускания груза до пола, силу натяжения T нити и кинетическую энергию K груза в момент удара о пол.

Решение:

Распределение сил для данного случая (рисунок 3).

Рисунок 3 – Распределение сил

По закону сохранения энергии

(1)

где угловая скорость ;

высота груза от пола ;

скорость падения груза ;

момент инерции сплошного цилиндрического барабана .

Подставив их значения в (1), получим

откуда

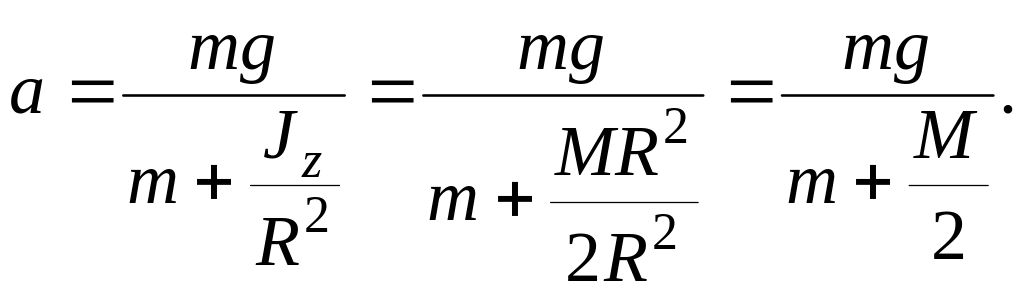
Время опускания груза до пола

, (2)

Уравнение динамики вращательного движения барабана

откуда сила натяжения нити где угловое ускорение , тогда сила натяжения нити

, (3)

Кинетическая энергия груза в момент удара о пол:

(4)

Подставим численные значения:

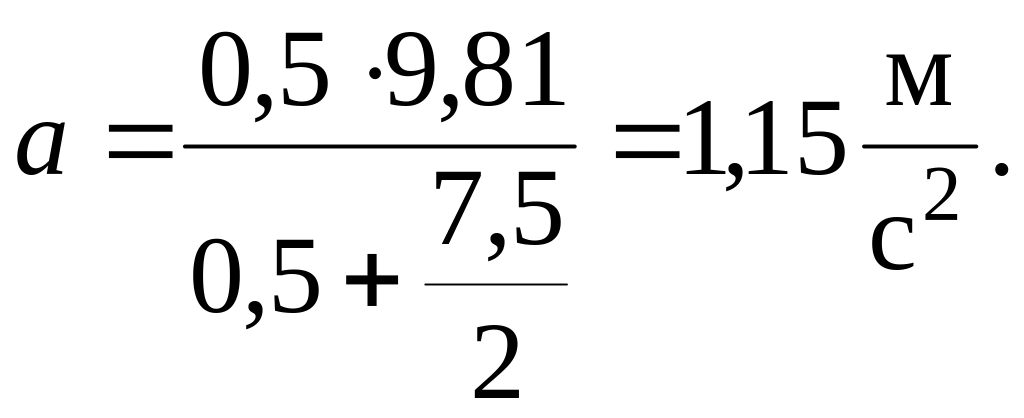
с.

Н.

Дж.

Ответ: t = 2 с; Т = 4,31 Н; Е_к = 1,32 Дж.

Задача 4. В сосуде вместимостью 5 л при нормальных условиях находится азот. Определите: 1) количество вещества ν; 2) массу m азота; 3) концентрацию n его молекул в сосуде; 4) массу m₀ одной молекулы азота.

Решение

Из уравнения Клапейрона-Менделеева

следует, что число молей

, (1)

Число молей , откуда масса азота

По основному уравнению молекулярно-кинетической теории давление азота в сосуде р_н =nkT_н,, где k = 1,38 ×10 Дж/К – постоянная Больцмана, откуда концентрация атомов азота

(2)

Масса одной молекулы азота равна

, (3)

Подставим численные значения.

моль.

кг.

м^-3.

кг.

Ответ: ν = 0,223 моль; m = 6,25×10^-3 кг; n = 2,69×10²⁵ м^-3 ; m₀ =4,7×10^-26 кг.

Задача 5. Определите массу азота, прошедшего вследствие диффузии через площадку S = 50 см² за время t = 20 с, если градиент плотности в направлении, перпендикулярном площадке, равен = 1 кг/м⁴. Температура азота Т = 290 К, а средняя длина свободного пробега его молекул равна <l> = 1 мкм.

Решение

По уравнению диффузии (закону Фика)

, где коэффициент диффузии ,

<l> = 10^-6 м, а средняя скорость молекул .

Тогда масса азота равна

.

Найдем численное значение m:

кг = 15,6 мг.

Ответ: m = 15,6 мг.

Задача 6. Азот, находившийся при температуре Т = 400 К, подвергся адиабатному расширению, в результате чего его объем увеличился в n = 5 раз, а внутренняя энергия уменьшилась на DU = - 4 кДж. Определить массу m азота.

Решение

При адиабатном процессе отсутствует теплообмен с окружающей средой и Q = 0. Из первого начала термодинамики получаем, что А DU.

Работа при адиабатном процессе равна ,

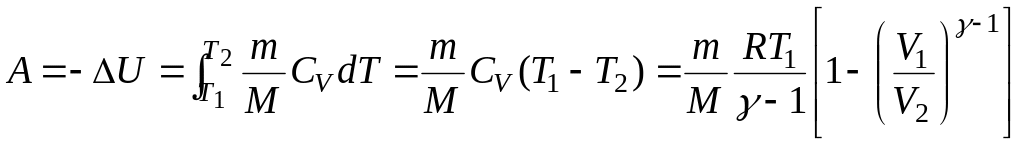учитывая, что показатель адиабаты .

Отсюда следует, что масса m азота равна

.

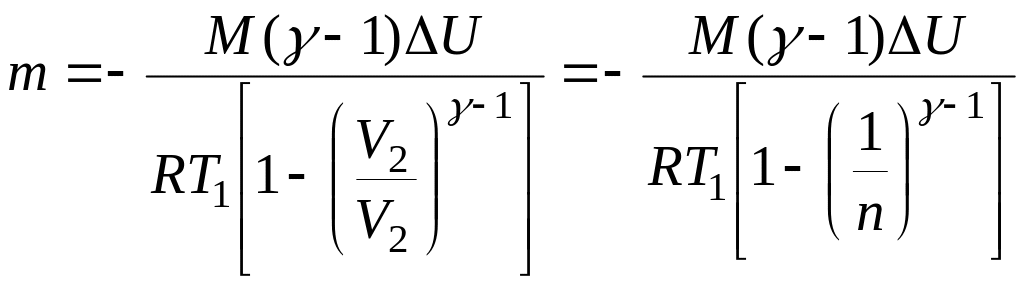Найдем численное значение m. Число степеней свободы для жестких двух-атомных молекул, каковыми являются молекулы азота, i = 5, поэтому показатель

адиабаты равен .

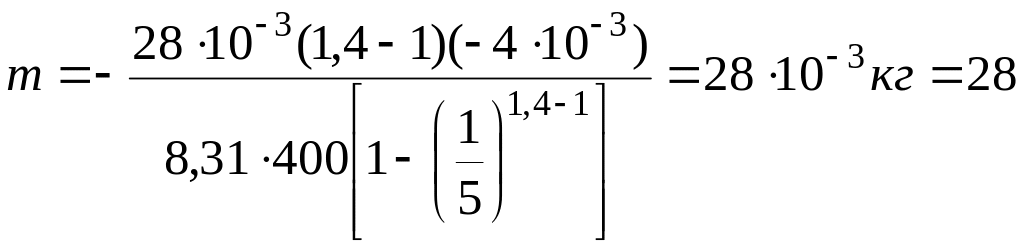г.

Ответ: m = 28 г.

Задача 7. В центре квадрата, в каждой вершине которого находится заряд равный 2,4 нКл, помещен отрицательный заряд q_o . Найти этот заряд, если на каждый заряд в вершине действует результирующая сила, равная 0,4 мН. Сторона квадрата 1 см (ε=1).

Решение:

Данный процесс удобно показать на рисунке 4.

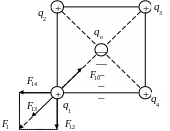
Рисунок 4 – Распределение сил между зарядами

Результирующая сила F, действующая на каждый из зарядов, находящихся в

вершинах квадрата, равна , где на основании закона Кулона

,

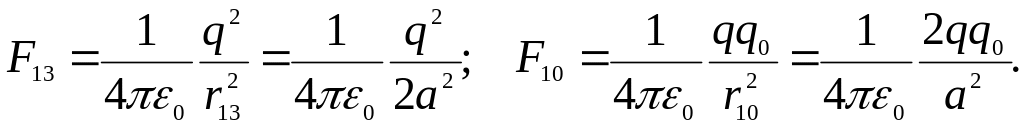
Отсюда:

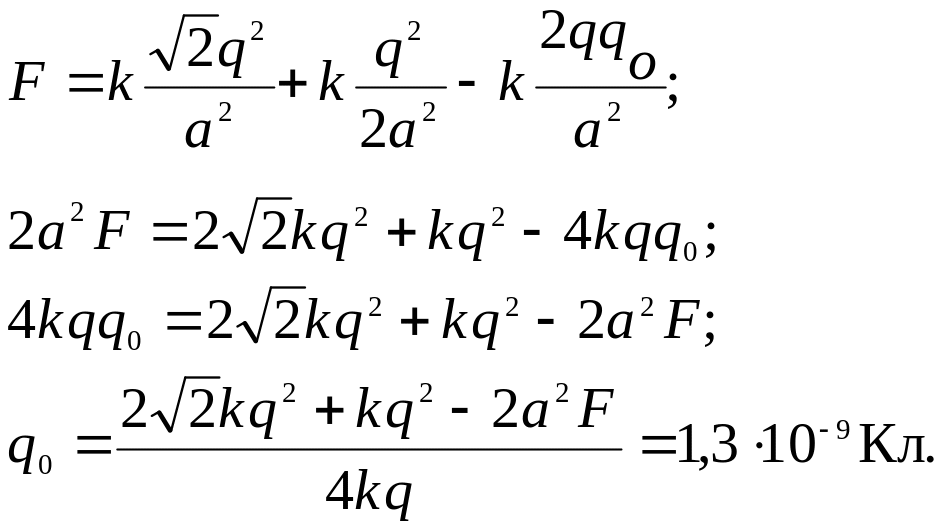
Задача 8. Два точечных заряда q₁ = 7,5 нКл и q₂ = -14,7 нКл расположены на расстоянии r = 5 см. Найти напряженность электрического поля в точке, находящейся на расстоянии а = 3 см от положительного заряда и b = 4 см от отрицательного заряда.

Решение:

Данный процесс удобно показать на рисунке 5.

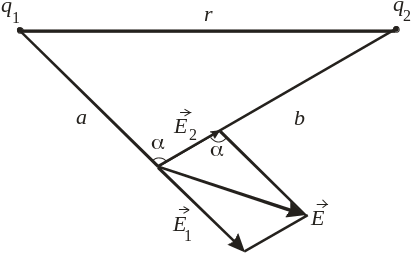
Рисунок 5 – С оставляющие напряженности электростатического поля

Каждый заряд в искомой точке пространства создает свое электрическое поле: напряженность поля положительного заряда q₁ направлена по силовой линии от заряда, напряженность поля отрицательного заряда q₂ - по силовой линии к заряду. Согласно принципу суперпозиции напряженность поля в искомой точке пространства равна

(1)

Модуль вектора можно определить по теореме косинусов как

. (2)

Напряженности поля, создаваемые в рассматриваемой точке пространства первым и вторым зарядами соответственно, равны

(3)

Косинус угла  между векторами и можно определить по теореме косинусов, примененной для треугольника расстояний а, b, r:

,

откуда . (4)

Подставив (3), (4) в (2), получим

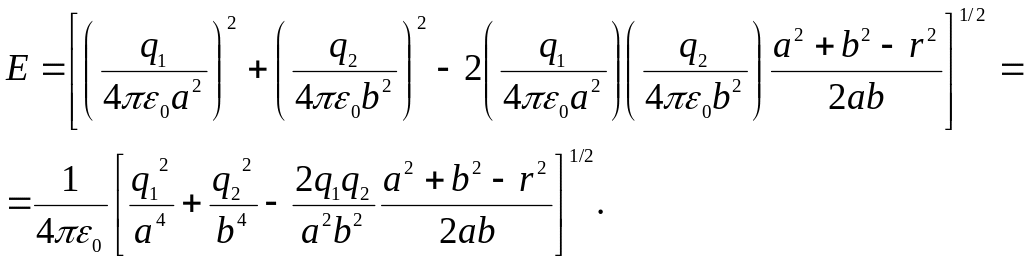(5)

Подставим в (5) численные значения:

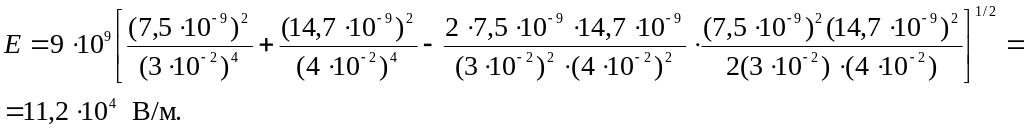Ответ: Е = 11,210⁴ В/м.

Задача 9. В цепь переменного тока частотой f = 50 Гц включена катушка длиной l = 30 см и площадью поперечного сечения S = 10 см², содержащая N = 1000 витков. Определите активное сопротивление катушки, если известно, что сдвиг фаз между напряжением и током  = 30⁰.

Решение

Тангенс сдвига фаз между напряжением и током в общем случае равен

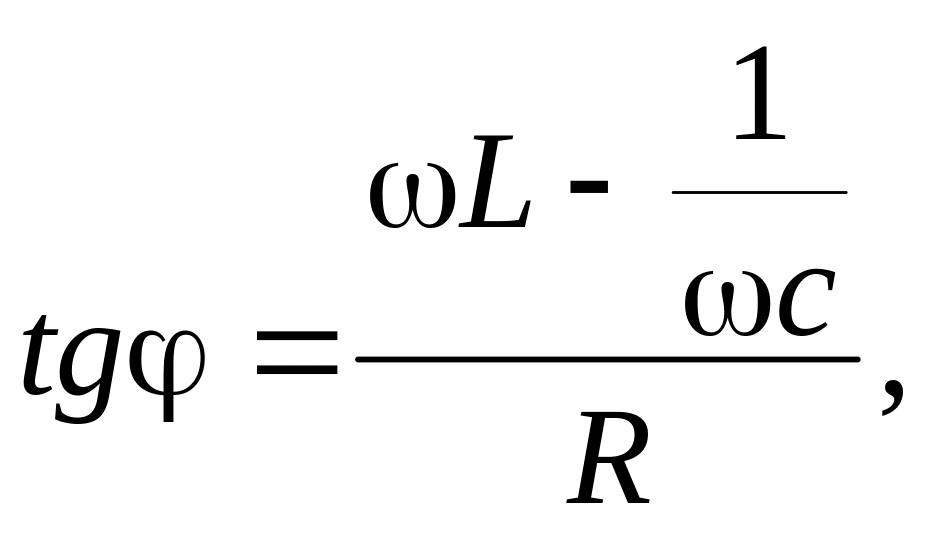
где круговая частота  = 2 f. Учитывая, что емкостное сопротивление , получаем, что ,

откуда Индуктивность катушки индуктивности

Активное сопротивление катушки

Подставим численные значения: Ом.

Ответ: R = 2,28 Ом.