Градиент

Пусть задано скалярное поле U(М)=U(x,y,z). Вектор с проекциями на оси , , называется градиентом величин U(в соответствующей точке) и обозначается так

Градиентом скалярной величины U в данной точке называется вектор, который по численному значению и направлению характеризует наибольшую скорость возрастания величины U.

Численное значение градиента

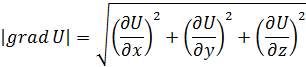
Пример:

Найти величину и направление градиента поля

в точке А(1,1,1)

в точке А(1,1,1)

Можно показать, что направление градиента совпадает с направлением нормали к поверхности уровня U(x,y,z)=0, проходящей через данную точку. Итак, скалярное поле U(M) порождает векторное поле градиента gradU.\

Производная в данном направлении

К ак мы говорили, частные производные f_x’(M₀) и f_y’(M₀) функции z=f(x,y) определяют в данной точке M₀(x₀,y₀) скорость изменения функции z при неизменном х или у. Геометрически это означает, что f_x’(M₀) и f_y’(M₀) определяют «крутизну» поверхности Q, уравнение которой z=f(x,y), в точке P₀(x₀,y₀,z₀), в направлении оси ох и оси оу (вдоль кривых и ).

Рассмотрим теперь скорость изменения z в точке M₀(x₀,y₀) в произвольном направлении, образующем некоторый угол с осью ох.

Геометрически это означает определение «кривизны» поверхности Q в точке P₀(x₀,y₀,z₀) в произвольном направлении вдоль кривой . Производная в заданном направлении является линейной комбинацией частных производных х:

Пример.

Вычислить в точке ( производную функции z= xy+lnx в направлении, соответствующему угол с осью ох

.

Видим, что функция z возрастает в точке в принятом нами направлении.

Касательная плоскость и нормаль к поверхности

О пределение: Касательной плоскостью к поверхности F(x,y,z)=0 в данной точке P называется плоскость, проходящая через точку P и содержащая в себе все касательные, построенные в точке Р ко всевозможным кривым, лежащим на поверхности и проходящим через точку Р.

Определение: Нормалью к поверхности α в точке Р называется прямая проходящая через точку Р и перпендикулярная к касательной плоскости, построенной в этой точке.

Касательная плоскость Т проходит через точку Р и перпендикулярна вектору N_p с координатам 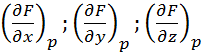, поэтому имеет следующий вид:

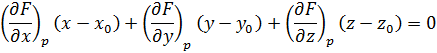
где , , - координаты точки Р.

Уравнение нормали:

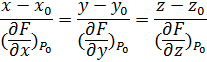
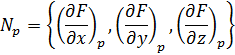
Пример

Составить уравнение касательной плоскости к поверхности

в точке Р(3,2,1)

Здесь ( ( =α)

Следовательно

Числовое значение производной в точке Р будет:

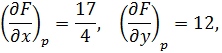
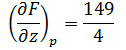
Уравнение касательной плоскости

и уравнением нормали(проходит через т.Р перпендикулярно касательным плоскости)

Экстремум функций многих переменных. Абсолютный экстремум.

Определение. Точка М₀ называется точкой максимума функции z(М),если значение функции в этой точке больше, чем её значение в любой другой точке некоторой окрестности точки М₀.

Аналогично, с заменой «больше» на меньше определяется точка min функции.

Из определения следует, что приращение функции всегда сохраняет знак:

(-) в точке max

(+) в точке min

Необходимый признак экстремума функции: В точке экстремума первый дифференциал функции обязательно должен быть обращен в 0.

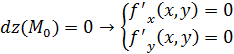
Достаточный признак.

Обозначим

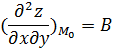
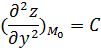
Тогда признаком наличия экстремума:

1) AC-B²>0 экстремумы есть, при этом max ,если A<0, min A>0

2) AC-B²<0 экстремумов нет

3)AC-B²=0 сомнительный случай

Для нахождения критической точки решим систему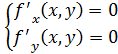

Пример 1.

Найти экстремумы функции

Найдем частную производную и решим систему.

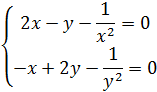
Система имеет единственное решение в точке x=1 у=1. Вычисляем вторые производные в М₀(1,1).

Используя достаточное условие экстремума 4*4+1>0 экстремум есть точка min,так как А>0 то min. По установленному x=1 у=1находим z_min=4

Пример 2.

Составим систему

Решим систему:х=0,у=0.

Вычислим производную второго порядка в точке (0,0)

Тогда AC-B²=1-1=0

Достаточные условия не соблюдаются. Перейдем к непосредственному исследованию функции этой точки. Возьмем приращение в окрестности точке М₀. Преобразуем . Видно, что в ноль не обращается, так как не равны нулю одновременно. И . А это значит, что функция z в точке М₀ имеет min.Из исходных уравнений находим z_min=1

14