
- •Функции нескольких переменных.
- •Предел функции.
- •Непрерывные функции.
- •Производные и дифференциалы функции нескольких переменных.
- •Частные производные
- •Частные дифференциалы.
- •Полный дифференциал.
- •Дифференциал сложной и неявной функции.
- •Дифференцирование неявной функции.
- •Градиент
- •Численное значение градиента
- •Производная в данном направлении
- •Касательная плоскость и нормаль к поверхности
- •Экстремум функций многих переменных. Абсолютный экстремум.
Функции нескольких переменных.
До сих пор мы изучали совместное изменение двух переменных, из которых одна зависима от другой. В науке и жизни нередки, однако, случаи, когда независимых переменных оказывается несколько.
Так, например, объем V кругового цилиндра есть функция от радиуса R его основания и от высоты цилиндра.
![]()
Или: по закону Ома напряжение в цепи электрического тока является функцией от силы тока и сопротивления.
![]()
Уточнение понятия функции нескольких независимых переменных проведем для случая двух переменных.
Определение:
величина z
называется функцией двух независимых
переменных x
и y,
если каждой паре ![]() ,
принадлежащей некоторой области G,
соответствует единственное определенное
числовое значение величины z.
,
принадлежащей некоторой области G,
соответствует единственное определенное
числовое значение величины z.
Область G называется областью определения функции z, а множество числовых значений, принятых z в этой области, называется областью значений z.
Функция
z
записывается так
![]()
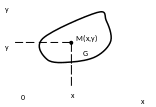 Пару
чисел
Пару
чисел ![]() ,будем
изображать в виде точки
,будем
изображать в виде точки ![]() координатной плоскости xOy.При
изменении значений х и у, т. М будет
двигаться по плоскости аргументов,
Причем каждому ее положению соответствует
определенное значение функции z.
Можно записать, что
координатной плоскости xOy.При
изменении значений х и у, т. М будет
двигаться по плоскости аргументов,
Причем каждому ее положению соответствует
определенное значение функции z.
Можно записать, что ![]() – функция точки М.
– функция точки М.
Пусть G – есть область определения функции z. Точка, расположенная на границе, - граничная точка. Совокупность всех граничных точек называется границей области.
Если добавить к области G её границу, то получим замкнутую область.
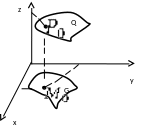 Рассмотрим
геометрическую интерпретацию функции
двух аргументов
.
Рассмотрим
геометрическую интерпретацию функции
двух аргументов
.
Тройка
чисел ![]() ,будет изображаться точкой
,будет изображаться точкой ![]() .
.
Если
точка ![]() будет двигаться в области G
, то точка Р опишет некоторую поверхность
Q.
Это и есть геометрический образ функции
.
будет двигаться в области G
, то точка Р опишет некоторую поверхность
Q.
Это и есть геометрический образ функции
.
Предел функции.
Определение:
число С называется пределом функции
![]() при
при ![]() ,
если при всяком
,
если при всяком ![]() можно указать такое число
можно указать такое число ![]() ,
что неравенство
,
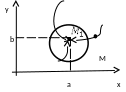
что неравенство ![]() ,будет справедливо для всех точек М,
лежащих в
,будет справедливо для всех точек М,
лежащих в ![]() окрестности точки
окрестности точки ![]() .
.
![]() или
или
![]()
Предел функции z не зависит от способа приближения точки М к ; он должен быть одним и тем же числом С при любом способе приближения М к .
Непрерывные функции.
Определение:
функция ![]() называется непрерывной в точке Р(а,b)
области определения G,
если функция z
определена в некоторой окрестности
этой точки, имеет предел при
называется непрерывной в точке Р(а,b)
области определения G,
если функция z
определена в некоторой окрестности
этой точки, имеет предел при ![]() ( то есть при
( то есть при ![]() )
и этот предел равен значению z
в точке Р.
)
и этот предел равен значению z
в точке Р.
![]() или
или
![]()
Точка Р является внутренней точкой области G.
Производные и дифференциалы функции нескольких переменных.
Частные производные
Дадим
аргументу х функции
приращение ![]() ,
сохраняя значение второго аргумента у
неизменным. Тогда функция z
получит приращение
,
сохраняя значение второго аргумента у
неизменным. Тогда функция z
получит приращение ![]() называется частным приращением функции
z
по аргументу х. Аналогично
называется частным приращением функции
z
по аргументу х. Аналогично ![]()
Отношения
![]() и
и ![]() дают нам среднюю скорость изменения
функции z
по аргументу х на отрезке
дают нам среднюю скорость изменения
функции z
по аргументу х на отрезке ![]() и по аргументу у на отрезке
и по аргументу у на отрезке ![]() .
.
И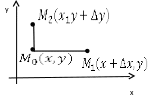 стинную
скорость в этих направлениях получим
переходя в обоих отношениях к пределу
при
стинную
скорость в этих направлениях получим
переходя в обоих отношениях к пределу
при ![]() и
и ![]() .Эти
пределы называются частными
производными функции z.
.Эти
пределы называются частными
производными функции z.
Определение: частной производной (первого порядка) функции аргументов х и у по одному из них, называется предел отношения соответствующего частного приращения функции z к приращению этого аргумента, когда последний стремится произвольным образом к нулю:
![]()
![]()
Частную производную можно обозначить
![]()
Вычислить частную производную.
Пример 1.
![]()
![]()
![]()
Пример 2.
![]()
![]()
![]()
![]()
Необходимым условием существования частной производной является непрерывность функции по соответствующим аргументам.
Пусть, например, есть частная производная в т. М(х,у).
![]()
Отсюда следует, что
![]()
Умножим
на ![]()
![]() здесь
здесь
![]() ,
т.е. z
есть непрерывная функция по аргументу
х.
,
т.е. z
есть непрерывная функция по аргументу
х.
Аналогично указывается непрерывность z по аргументу у.
Как
видно из примеров частные производные
![]() функции
являются вновь функциями от обоих
аргументов х и у. Значит можно найти
частную производную от их частных
производных
функции
являются вновь функциями от обоих
аргументов х и у. Значит можно найти
частную производную от их частных
производных
![]()
![]()
![]()
Эти производные называются частными производными второго порядка.
Пример: вычислить частную производную первого и второго порядков.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Надо
заметить, что ![]() .
Это не случайное обстоятельство.
.
Это не случайное обстоятельство.
Теорема. Результат дифференцирования не зависит от порядка выполнения дифференцирования.
Согласно теореме будут равны между собой следующие частные производные:
![]()
