Содержание
1.Введение
2.Прямая в пространстве
3.Как составить уравнения прямой в пространстве?
4.Параметрические уравнения прямой в пространстве
5.Прямая заданная пересечением двух плоскостей
6.Задаче и решение
7.Прямая и плоскось
8.Вывод
9.Литература
Введение
На лекции мы изучим положение прямой в пространстве, взаимное расположение прямых в пространстве, взаимное расположение прямых и плоскостей. Положение прямой в пространстве можно характеризовать различными способами. Например, можно указать: две точки прямой; две плоскости, пересекающиеся по этой прямой; точку на прямой и вектор, параллельный этой прямой, и т. д. Но прежде всего мы изучим задание линии в пространстве как пересечении я двух поверхностей и в параметрической форме.
Прямая в пространстве
Прямая линия в пространстве является одной из основных фигур в геометрии. Она состоит из бесконечного множества абстрактных объектов, у которых отсутствует объем, площадь, длина и какие-либо другие характеристики. Данные нульмерные объекты также служат фундаментальными фигурами в геометрии и именуются точками. Прямая в пространстве аналогична той, которую проводят на имеющейся плоскости. При помощи воображения должны быть отмечены две точки. Между ними, а также за их пределы до бесконечности при помощи линейки проводится линия. Это и есть прямая в пространстве. На этой линии можно обозначить отрезок или точку.
Как составить уравнения прямой в пространстве?
Аналогично «плоской» прямой, существует несколько способов, которыми мы можем задать прямую в пространстве. Начнём с канонов – точки и направляющего вектора прямой:
Канонические уравнения прямой
Если
известна некоторая точка пространства 
,
принадлежащая прямой, и направляющий
вектор 
данной
прямой, то канонические уравнения
этой прямой выражаются формулами:
Приведённая
запись предполагает, что координаты
направляющего вектора 
не
равны нулю.
Что делать, если одна или две координаты
нулевые, мы рассмотрим чуть позже.
Как и в статье Уравнение плоскости, для простоты будем считать, что во всех задачах урока действия проводятся в ортонормированном базисе пространства.
Пример 1
Составить
канонические уравнения прямой по
точке 
и
направляющему вектору 
Решение:
Канонические уравнения прямой составим
по формуле:
Ответ: 
И ежу понятно… хотя, нет, ежу не понятно вообще ничего.
Что
следует отметить в этом очень простом
примере? Во-первых, полученные уравнения
НЕ НАДО сокращать на единицу: 
.
Сократить, точнее, можно, но это непривычно
режет глаз и создаёт неудобства в ходе
решения задач.
А во-вторых, в аналитической геометрии неизбежны две вещи – это проверка и зачёт:
На всякий случай смотрим на знаменатели уравнений и сверяемся – правильно ли там записаны
координаты направляющего вектора . Нет, не подумайте, у нас не урок в детском садике «Тормозок». Данный совет очень важен, поскольку позволяет полностью исключить ошибку по невнимательности. Никто не застрахован, а вдруг неправильно переписали? Наградят премией Дарвина по геометрии.
Далее
подставляем координаты точки
в
найденные уравнения:
Получены
верные равенства, значит, координаты
точки 
удовлетворяют
нашим уравнениям, и сама точка действительно
принадлежит данной прямой.
Проверка очень легко (и быстро!) выполняется устно.
В
ряде задач требуется найти какую-нибудь
другую точку 
,
принадлежащую данной прямой. Как это
сделать?
Берём
полученные уравнения
и
мысленно «отщипываем», например, левый
кусочек: 
.
Теперь этот кусочек приравниваем к
любому числу (помним,
что ноль уже был), например, к единице: 
.
Так как
,
то и два других «куска» тоже должны быть
равны единице. По сути, нужно решить
систему:
Проверим,
удовлетворяет ли найденная
точка 
уравнениям
:
Выполним
чертёж в прямоугольной системе координат.
Заодно вспомним, как правильно откладывать
точки в пространстве:
Строим
точку
:
–
от начала координат в отрицательном
направлении оси 
откладываем
отрезок первой координаты 
(зелёный
пунктир);
– вторая координата 
нулевая,
поэтому «не дёргаемся» с оси
ни
влево, ни вправо;
– в соответствие с
третьей координатой 
отмеряем
три единицы вверх (фиолетовый пунктир).
Строим
точку
:
отмеряем две единицы «на себя» (желтый
пунктир), одну единицу вправо (синий
пунктир) и две единицы вниз (коричневый
пунктир). Коричневый пунктир и сама
точка
наложились
на координатную ось, обратите внимание,
что они находятся в нижнем полупространстве
и ПЕРЕД осью
Сама
прямая 
проходит
над осью
и,
если меня не подводит глазомер, над
осью 
.
Не подводит, убедился аналитически.
Если бы прямая
проходила
ЗА осью
,
то следовало бы стереть ластиком частичку
линии
сверху
и снизу точки скрещивания.
У
прямой бесконечно много направляющих
векторов, например:
(красная
стрелка)
Получился
в точности исходный вектор
,
но это чистая случайность, такую уж я
выбрал точку
.
Все направляющие векторы прямой
коллинеарны, и их соответствующие
координаты пропорциональны (более
подробно – см. Линейная
(не) зависимость векторов. Базис векторов).
Так, векторы 
тоже
будут направляющими векторами данной
прямой.
Дополнительную информацию о построении трёхмерных чертежей на клетчатой бумаге можно найти в начале методички Графики и свойства функций. В тетради разноцветные пунктирные дорожки к точкам (см. чертёж) обычно тонко прочерчивают простым карандашом тем же пунктиром.
Разберёмся
с частными случаями, когда одна или две
координаты направляющего вектора
нулевые. Попутно продолжаем тренировку
пространственного зрения, которая
началась в начале урока Уравнение
плоскости.
И вновь я расскажу вам сказку о голом
короле – нарисую пустую систему координат
и буду убеждать вас, что там есть
пространственные прямые =)
Проще перечислить все шесть случаев:
1)
Для точки
и
направляющего вектора 
канонические
уравнения прямой распадаются на
три отдельных уравнения: 
.
Или
короче: 
Пример
2:
составим уравнения прямой по точке 
и
направляющему вектору 
:
Что
это за прямая? Направляющий вектор
прямой
коллинеарен
орту 
,
значит, данная прямая будет параллельна
оси
.
Канонические уравнения следует понимать
так:
а) 
–
«игрек» и «зет» постоянны,
равны конкретным
числам;
б)
переменная «икс» может принимать любые
значения: 
(на
практике данное уравнение, как правило,
не записывают).
В
частности, уравнения 
задают
саму ось
.
Действительно, «икс» принимает любое
значение, а «игрек» и «зет» всегда равны
нулю.
Рассматриваемые
уравнения можно интерпретировать и
другим образом: посмотрим, например, на
аналитическую запись оси абсцисс:
.
Ведь это уравнения двух плоскостей!
Уравнение
задаёт
координатную плоскость 
,
а уравнение 
–
координатную плоскость 
.
Правильно думаете – данные координатные
плоскости пересекаются по оси
.
Способ, когда прямая в пространстве
задаётся пересечением двух плоскостей,
мы рассмотрим в самом конце урока.
Два похожих случая:
2)
Канонические уравнения прямой, проходящей
через точку
параллельно
вектору 
,
выражаются формулами 
.
Такие
прямые будут параллельны координатной
оси
.
В частности, уравнения 
задают
координатную саму ось ординат.
3)
Канонические уравнения прямой, проходящей
через точку
параллельно
вектору 
,
выражаются формулами 
.
Данные
прямые параллельны координатной оси 
,
а уравнения 
задают
саму ось аппликат.
Загоним в стойло вторую тройку:
4)
Для точки
и
направляющего вектора 
канонические
уравнения прямой распадаются на
пропорцию 
и уравнение
плоскости 
.
Пример
3:
составим уравнения прямой по точке 
и
направляющему вектору 
:
Разберём
суть полученной записи. Уравнение 
задаёт
плоскость в пространстве, причём данная
плоскость будет параллельна «родной»
координатной плоскости
.
Из пропорции 
легко
выразить уравнение «плоской» прямой,
единственное, эта прямая будет находиться
не на плоскости
,
а на высоте 
.
Если
высота нулевая: 
,
то уравнения принимают вид 
,
и вот это уже в точности наша «плоская»
прямая, лежащая в плоскости
.
Таким образом, рассмотренный случай задаёт прямую, параллельную координатной плоскости . Действительно, задумайтесь, ведь направляющий вектор параллелен данной плоскости, ведь «зетовая» координата равна нулю.
5)
Прямая, заданная точкой
и
направляющим вектором 
,
параллельна координатной плоскости
,
и её канонические уравнения выражаются
формулами: 
.
В
частности, уравнения 
определяют
прямую, лежащую в плоскости
.
6)
Прямая, заданная точкой
и
направляющим вектором 
,
параллельна координатной плоскости 
,
и её канонические уравнения выражаются
формулами: 
.
В
частности, уравнения 
определяют
прямую, лежащую в плоскости
.
Настала пора хорошо закусить:
Пример 4
Записать канонические уравнения прямой, если известна точка и направляющий вектор данной прямой.
а) 
б) 
в)
Записать уравнения прямой, проходящей
через точку 
параллельно
оси
.
Это примеры для самостоятельного решения, ответы в конце урока.
Постарайтесь не пренебрегать примерами данного урока! Задачи вроде бы элементарны, но если на них забить, то в дальнейшем появятся серьёзные затруднения. Причём, в простых вещах.
Как составить уравнения пространственной прямой по двум точкам?
Если
известны две точки пространства 
,
то уравнения прямой, проходящей через
данные точки, выражаются формулами:
Унылый
частный случай предыдущего параграфа.
И в самом деле, вектор 
является
направляющим вектором прямой.
По возможности, рекомендую не пользоваться данными формулами. Хорошо-то оно, всё хорошо, но только до тех пор, пока знаменатели без нулей. Не буду объяснять все тонкости, но рекомендую придерживаться следующего алгоритма решения:
Пример 5
Составить
уравнения прямой, проходящей через
точки 
.
Решение:
Найдём направляющий вектор прямой:
Уравнения
прямой составим по точке 
(можно
было выбрать точку 
)
и направляющему вектору 
:
Ответ: 
В
принципе, можно было сократить знаменатели
пропорции на 2 и записать ответ в виде 
,
но в
данном случае
надобности в этом нет никакой.
Выполним проверку:
Подставим
координаты точки
в
полученные уравнения:
Получены
верные равенства.
Подставим
координаты точки 
:
Получены
верные равенства.
Вывод: канонические уравнения прямой составлены правильно.
Параметрические уравнения прямой в пространстве
Параметрические уравнения, конечно, не альфа и омега пространственной геометрии, но рабочий муравей многих задач. Причём, этот вид уравнений часто применяется неожиданно, и я бы сказал, изящно.
Если известна точка , принадлежащая прямой, и направляющий вектор данной прямой, то параметрические уравнения этой прямой задаются системой:
О самом понятии параметрических уравнений я рассказывал на уроках Уравнение прямой на плоскости и Производная параметрически заданной функции.
Всё проще пареной репы, поэтому придётся приперчить задачу:
Пример 6
Составить
параметрические уравнения следующих
прямых:
Решение: Прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.
а)
Из уравнений 
снимаем
точку и направляющий вектор: 
.
Точку можно выбрать и другую (как это
сделать – рассказано выше), но лучше
взять самую очевидную. Кстати, во
избежание ошибок, всегда подставляйте
её координаты в уравнения.
Составим
параметрические уравнения данной
прямой:
Удобство
параметрических уравнений состоит в
том, что с их помощью очень легко находить
другие точки прямой. Например, найдём
точку 
,
координаты которой, скажем, соответствуют
значению параметра 
:
Таким
образом: 
б)
Рассмотрим канонические уравнения 
.
Выбор точки здесь несложен, но
коварен: 
(будьте
внимательны, не перепутайте координаты!!!).
Как вытащить направляющий вектор? Можно
порассуждать, чему параллельна данная
прямая, а можно использовать простой
формальный приём: в пропорции находятся
«игрек» и «зет», поэтому запишем
направляющий вектор 
,
а на оставшееся место поставим ноль: 
.
Составим
параметрические уравнения прямой:
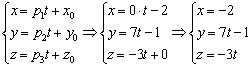
в)
Перепишем уравнения 
в
виде 
,
то есть «зет» может быть любым. А если
любым, то пусть, например, 
.
Таким образом, точка 
принадлежит
данной прямой. Для нахождения направляющего
вектора используем следующий формальный
приём: в исходных уравнениях
находятся
«икс» и «игрек», и в направляющем векторе
на данных
местах
записываем нули: 
.
На оставшееся место ставим единицу: 
.
Вместо единицы подойдёт любое число,
кроме нуля.
Запишем
параметрические уравнения прямой:
Прямая, заданная пересечением двух плоскостей
Если
плоскости 
пересекаются,
то
система линейных уравнений 
задаёт
прямую в пространстве.
То есть прямая задана уравнениями двух плоскостей. Типовая и распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:
Пример 7
Записать
канонические уравнения прямой 
Решение: Чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей….
1)
Сначала найдём какую-либо точку,
принадлежащую данной прямой. Как это
сделать? В системе уравнений нужно
обнулить какую-нибудь координату.
Пусть
,
тогда получаем систему двух линейных
уравнений с двумя неизвестными: 
.
Почленно складываем уравнения и находим
решение системы:
Таким
образом, точка 
принадлежит
данной прямой. Обратите внимание на
следующий технический момент: желательно
найти точку с целыми координатами.
Если бы в системе мы обнулили «икс» или
«зет», то не факт, что получилась бы
«хорошая» точка без дробных координат.
Такой анализ и подбор точки следует
проводить мысленно или на черновике.
Выполним
проверку: подставим координаты точки
в
исходную систему уравнений: 
.
Получены верные равенства, значит,
действительно 
.
2)
Как найти направляющий вектор прямой?
Его нахождение наглядно демонстрирует
следующий схематический чертёж:
Направляющий
вектор нашей прямой ортогонален
нормальным векторам плоскостей. А
если 
,
то вектор «пэ» найдём как векторное
произведение векторов
нормали: 
.
Из
уравнений плоскостей 
снимаем
их векторы нормали:
И
находим направляющий вектор прямой:
Как проверить результат, рассматривалось в статье Векторное произведение векторов.
3)
Составим канонические уравнения прямой
по точке
и
направляющему вектору 
:
Ответ: 
Пример
8; Решение:
Найдём какую-нибудь точку, принадлежащую
данной прямой. Пусть
,
тогда: 
.
Точка 
.
Найдём направляющий вектор прямой,
используем формулу:
Составим
канонические уравнения прямой по
точке 
и
направляющему вектору 
:
Ответ: 
Прямая и плоскость
Простейшими фигурами в пространстве являются точка, прямая и плоскость.
Точки
обозначают прописными буквами латинского
алфавита: 
, 
, 
, 
и
т. д.
Прямые
обозначают или строчными буквами
латинского алфавита 
, 
, 
, 
или
двумя прописными буквами 
, 
и
т. д.
Плоскости
обозначают строчными буквами греческого
алфавита 
, 
, 
и
т. д.
На рисунках плоскости изображают в виде произвольной области, а чаще в виде параллелограмма.
На рисунке 9.1 изображены плоскости , и .
Если
точка
принадлежит
плоскости
,
то пишут: 
;
если точка
не
принадлежит этой плоскости, то
пишут: 
(рис.
9.2).
Если
прямая с принадлежит плоскости
,
то пишут: 
;
если прямая
не
принадлежит этой плоскости, то
пишут: 
(рис.
9.3).
Основные свойства взаимного расположения точек, прямых и плоскостей в пространстве выражают аксиомы стереометрии и следствия из них.
Аксиомы стереометрии
1. Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
На рисунке 9.4 через точки , и проведена плоскость .
2. Если две точки прямой принадлежат плоскости, то все точки этой прямой принадлежат данной плоскости.
На рисунке 9.5 точки и прямой принадлежат плоскости , следовательно, прямая принадлежит плоскости .
3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей.
На рисунке 9.6 плоскости и имеют общую точку , принадлежащую прямой , следовательно, имеют общую прямую .
Следствия из аксиом
1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну. На рисунке 9.7 через прямую и точку проведена плоскость .
2. Через две пересекающиеся прямые можно провести плоскость, и притом только одну. На рисунке 9.8 через пересекающиеся прямые и проведена плоскость .
Взаимное расположение прямых в пространстве
Две прямые в пространстве могут пересекаться, быть параллельными, скрещиваться или совпадать.
Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются. На рисунке 9.9 прямые и параллельны.
Углом между двумя пересекающимися прямыми в пространстве называется наименьший из углов, образованных лучами этих прямых с вершиной в точке их пересечения. На рисунке 9.10 прямые и пересекаются под углом .
Две прямые называются перпендикулярными, если угол между ними прямой.
Две прямые в пространстве скрещиваются, если не существует плоскости, в которой они обе лежат.
Признак скрещивающихся прямых: если одна из двух прямых лежит в некоторой плоскости, а вторая прямая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещивающиеся.
На рисунке 9.11 изображены скрещивающиеся прямые и .
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
На рисунке 9.12 прямая параллельна прямой , – угол между скрещивающимися прямыми и .
Взаимное расположение прямых и плоскостей
В пространстве прямая может пересекать плоскость, быть ей параллельной или лежать в плоскости.
На рисунке 9.13 прямая пересекает плоскость в точке .
На рисунке 9.14 прямая параллельна плоскости , а прямая лежит в этой плоскости.
Плоскость и прямая, не принадлежащая плоскости, параллельны, если они не имеют общих точек.
Признак параллельности прямой и плоскости: если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, принадлежащей этой плоскости, то она параллельна плоскости.
На рисунке 9.14 прямая принадлежит плоскости , а прямая параллельна прямой и не принадлежит плоскости , следовательно, прямая параллельна плоскости .
Если плоскость содержит прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой. На рисунке 9.15 плоскость содержит прямую , параллельную плоскости , и пересекает плоскость , следовательно, линия пересечения этих плоскостей параллельна прямой .
Если через каждую из двух параллельных прямых проведены пересекающиеся плоскости, то линия их пересечения параллельна данным прямым. На рисунке 9.16 через две параллельные прямые и проведены пересекающиеся плоскости и , следовательно, линия пересечения этих плоскостей параллельна прямым и .
Взаимное расположение плоскостей в пространстве
Две плоскости в пространстве могут совпадать, быть параллельны или пересекаться.
Две плоскости параллельны, если они не имеют общих точек.
Признак параллельности плоскостей: если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
На рисунке 9.17 пересекающиеся прямые и принадлежат плоскости , а пересекающиеся прямые и – плоскости . При этом прямая параллельна прямой и прямая параллельна прямой . Следовательно, данные плоскости параллельны.
Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, принадлежащей плоскости.
Признак перпендикулярности прямой и плоскости: если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
На рисунке 9.18 прямая перпендикулярна каждой из двух пересекающихся прямых и , принадлежащих плоскости , следовательно, прямая перпендикулярна данной плоскости.
Свойства прямой, перпендикулярной плоскости
1. Два различных перпендикуляра к плоскости параллельны.
На
рисунке 9.19 прямые
и
перпендикулярны
плоскости
,
следовательно, 
.
2. Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.
На рисунке 9.20 плоскости и параллельны. Прямая перпендикулярна плоскости , следовательно, она перпендикулярна и плоскости .
Прямая, пересекающая плоскость, но не перпендикулярная к ней, называется наклонной к плоскости.
На рисунке 9.21 прямая – наклонная к плоскости .
Теорема о трех перпендикулярах. Для того чтобы прямая, лежащая в плоскости, была перпендикулярна наклонной к плоскости, необходимо и достаточно, чтобы она была перпендикулярна проекции этой наклонной на плоскость.
На рисунке 9.21 прямая – наклонная к плоскости, прямая – проекция этой наклонной на плоскость
и 
.
Тогда 
.
Углом между прямой и плоскостью называют угол между прямой и ее проекцией на плоскость. На рисунке 9.22 прямая – наклонная к плоскости, прямая – проекция этой наклонной на плоскость, следовательно, угол – угол между прямой и плоскостью.
Двугранным углом называют угол, образованный двумя полуплоскостями с общей границей. Прямую, которая является общей границей этих полуплоскостей, называют ребром двугранного угла, а полуплоскости с общим ребром – гранями двугранного угла.
На рисунке 9.23 изображен двугранный угол. Полуплоскости и – грани этого угла, прямая – ребро.
В результате пересечения двух плоскостей образуется четыре двугранных угла (рис. 9.24).
Двугранный угол измеряется соответствующим линейным углом. Линейным углом двугранного угла называют угол между перпендикулярами, проведенными в каждой грани к ребру.
На рисунке 9.25 угол – линейный угол двугранного угла.
Двугранный
угол может иметь любое значение от 
до
.
Если линейный угол двугранного угла
равен 
,
то плоскости перпендикулярны.
Признак перпендикулярности плоскостей: если плоскость содержит перпендикуляр к другой плоскости, то она перпендикулярна этой плоскости.
На рисунке 9.26 плоскости и перпендикуярны
Вывод
В разделе прямая на плоскости мы дали представление о точке и прямой на плоскости. Прямую линию в пространстве следует представлять абсолютно аналогично: мысленно отмечаем две точки в пространстве и проводим с помощью линейки линию от одной точки до другой и за пределы точек в бесконечность.Все обозначения точек, прямых и отрезков в пространстве аналогичны случаю на плоскости.Вообще, прямая линия целиком принадлежит некоторой плоскости в пространстве. Это утверждение вытекает из аксиом: через две точки проходит единственная прямая;если две точки прямой лежат в некоторой плоскости, то все точки прямой лежат в этой плоскости.Существует еще одна аксиома, которая позволяет рассматривать прямую в пространстве как пересечение двух плоскостей: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскости.
Литература
Высшая математика для экономистов: Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. 2-е изд., перераб. и доп. – М.: ЮНИТИ, 2003.
Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. — М., Высшая школа, 2002.
Гмурман В. Е. Теория вероятностей и математическая статистика. — М., Высшая школа, 2001.
Минорский В. П. Сборник задач по высшей математике. — М.: Наука, 2002
Теория вероятностей и математическая статистика : учебник / В.А. Колемаев, В.Н. Калинина. – 3-е изд., перераб. и доп. – М.:КНОРУС, 2009.
Шипачев В.С. Высшая математика. — М., Высшая школа, 2002.
Шипачев В.С. Сборник задач по высшей математике. — М., Высшая школа, 2006.
Средний мозг человека
Средний мозг является древним отделом головного мозга, включенным в его ствол. В него входит древний зрительный центр. Средний мозг располагается ниже коры головного мозга и выше заднего мозга, находясь как бы в самом центре головного мозга. Каудально средний мозг примыкает к заднему мозгу, а рострально к промежуточному мозгу. В вентральной части среднего мозга располагаются так называемые ножки мозга, большая часть которых занята пирамидными путями. В среднем мозге между ножками размещается межножковая ямка, из которой берет начало III глазодвигательный нерв. Глубоко в межножковой ямке находится заднее продырявленное вещество.
В состав среднего мозга входят: крыша среднего мозга (tectum), нижний бугорок (inferior colliculus), двухолмие (superior colliculi), мозговые ножки (cerebral peduncle), тегментум среднего мозга (midbrain tegmentum), черное вещество (substantia nigra), ножка мозга (crus cerebri). Следует отметить, что видимой границы с промежуточным мозгом нет.
Средний мозг представляет собой часть ствола головного мозга. Черное вещество среднего мозга тесно связано с опорно-двигательной системой путей базальных ганглиев. В черном веществе и в вентральной части покрышки происходит выработка дофамина, который играет важную роль в мотивации и возбуждении. Средний мозг передает зрительную и слуховую информацию.
Четверохолмие
Четверохолмие среднего мозга представляет собой две пары нижних и верхних холмиков. Верхние пары являются зрительными, а нижние пары слуховыми. при этом верхние пары холмиков несколько крупнее нижних пар. Данные холмики имеют связь со структурами промежуточного мозга, называемыми коленчатыми телами. При этом верхние холмики связаны с латеральными, а нижние холмики с медиальными. Из задней поверхности среднего мозга выходит блоковый нерв. Четыре твердых доли помогают пересекать под прямым углом несколько зрительных волокон. Слуховые ядра располагаются внутри нижних холмиков.
Мозговые ножки
Мозговые ножки представляют собой парные структуры, которые располагаются на брюшной стороне мозгового водопровода. Они переносят тегментум на дорсальную сторону. Средняя часть мозга содержит черное вещество, представляющее собой тип базального ядра. Черное вещество является единственной частью мозга, содержащей меланин. Между ножками располагается межножковая ямка. которая заполнена спинномозговой жидкостью, представляет собой как бы смывной бачок. Глазодвигательный нерв выходит между ножек, а блоковый нерв заметно обтекает внешние стороны ножек. Глазодвигательный нерв (парасимпатически) отвечает за сужение зрачка и за некоторые движения глаз.
Строение среднего мозга в разрезах
При горизонтальном разрезе среднего мозга на уровне верхнего холмика, наблюдается красное ядро, ядра глазодвигательного нерва и связанные с ними ядра Эдингер-Вестфаля, мозговые ножки, а также черное вещество.
При горизонтальном разрезе среднего мозга на уровне нижнего холмика также наблюдается черное вещество, также отчетливо видны ядра блокового нерва и перекрестие верхних
мозжечковых ножек. В обоих случаях наблюдается водопровод мозга, соединяющий третий и четвертый желудочки и околоводопроводное серое вещество.