4. Алгоритм траекторного управления [6]

Оптимальное управление полётом ЛА по маршруту осуществляется с помощью алгори-тма траекторного управления (АТУ), который представлен на рис.2. АТУ реализуется в БЦВМ.

Входными параметрами АТУ являются траекторные параметры ЛА относительно теку-щей ЛЗП и следующей ЛЗП: S, Z – ортодромические координаты ЛА; Z_max – максимальное допустимое боковое уклонение для использования в законе управления _З=k_Z Z+k_Ż Ż; ФПУ – фактический путевой угол; V – скорость ЛА; H – высота полёта; H_З – заданная высота полё-та; ЗПУ_i – заданный путевой угол i-й ЛЗП; ЗПУ_i+1 – заданный путевой угол (i+1)-й ЛЗП.

Выходными функциями АТУ являются: закон управления углом крена _З=k_Z Z+k_Ż Ż и за-кон управления углом тангажа _З.

S_У = S_У(V, H)

1

Нет

2

Да

Нет

ΔФПУ_i = ФПУ_i+1 – ФПУ_i

6

3

Да

_З = _З (ФПУ, ЗПУ_i, Z)

4

_З = k_Z Z+k_Ż Ż

5

_З = _З (ΔФПУ_i, ЗПУ_i, V, H)

7

_З = _З (ΔH, ΔH₂)

ΔH = H – H_З

8

10

9

Нет

Нет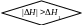

Да

Да

_З = _З (ΔH, ΔH₁)

11

12

_З = _З (ΔH, Δ , Δ )

13

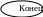
Рис.2. Блок-схема алгоритма траекторного управления.

Сигналы V и H позволяют рассчитать линейное упреждение разворота S_у (блок 1). При S >S_у АТУ обеспечивает режим стабилизации по боковому отклонению Z от ЛЗП, причём, при больших отклонениях, когда |Z| >Z_max (блок 3), обеспечивается перевод ЛА на траекто-рию сближения с ЛЗП. Расчёт _З при этом осуществляется с учётом параметров ФПУ, ЗПУ_i и Z, поскольку отпадает необходимость в сигнале Ż для демпфирования боковых колебаний из-за необходимости скорейшего сближения с ЛЗП (блок 4). При |Z| ≤Z_max АТУ обеспечивает управление ЛА по закону _З=k_Z Z+k_Ż Ż, при этом устойчивость траекторного управления обес-печивается тем, что кроме отклонения Z используется производная по времени Ż, которая обеспечивает демпфирование боковых колебаний (блок 5).

При S ≤S_у обеспечивается расчёт _З в зависимости от разности заданных путевых углов i-й и (i+1)-й ЛЗП, а также в зависимости от скорости и высоты полёта V и H (блоки 6 и 7).

Управление в продольной плоскости обеспечивается путём стабилизации высоты отно-сительно H_З. Вычисление _З осуществляется в зависимости от отклонений высоты полёта от заданной с помощью трёх различных соотношений (блоки 11, 12, 13). При больших отклоне-ниях высоты ΔH от заданной (блоки 9, 10) в закон управления по тангажу входят только по-зиционные параметры (блоки 11, 12), а при малых отклонениях – также и производные от ΔH, что обеспечивает устойчивость процесса стабилизации высоты (блок 13).

5. Математическое моделирование полёта по маршруту [7]

В программе OTU моделирование полёта ЛА по маршруту производится численным интегрированием системы дифференциальных уравнений, которая состоит из уравнений по-лёта в боковой плоскости и уравнений навигации в ортодромической системе координат.

Уравнения динамики полёта ЛА в боковой плоскости вместе с уравнением системы ав-томатического управления (САУ) имеют вид:

(11)

(12)

(13)

(14)

где ω_х, ω_у – проекции вектора угловой скорости на оси связанной системы координат (ССК); – переменная составляющая проекции угловой скорости на ось Y ССК; V – воздушная скорость ЛА;  – угол крена; _З – заданный угол крена; β – угол скольжения;  – курсовой угол ЛА (угол между вектором V и ЛЗП); g(Н) – ускорение свободного падения на высоте Н; , , , , – приведённые аэродинамические коэффициенты; ξ _х , ξ _у – коэф-фициенты демпфирования собственных колебаний системы ЛА–САУ относительно осей Х и Y ССК; Ω _х , Ω _у – угловые частоты собственных колебаний системы ЛА–САУ относительно осей Х и Y ССК; Т – постоянная времени интегро-дифференцирующего звена в канале курса САУ.

Коэффициенты дифференциальных уравнений (11)–(14) определяются с помощью вы-ражений = а₃ q; = а₄ q; = а₆ q; = а₅ q; = а₂ q₁, где q= ; q₁= .

Коэффициенты, входящие в вышеприведённые выражения, являются константами и оп-ределяются через аэродинамические, геометрические и инерционные характеристики ЛА и характеристики САУ:

где , , , , – аэродинамические коэффициенты ЛА; S – площадь крыла; l – – характеристический размер ЛА; m – масса ЛА; I _x , I _y – моменты инерции ЛА относительно осей симметрии ЛА.

Коэффициенты демпфирования собственных колебаний системы ЛА–САУ

Угловые частоты собственных колебаний системы ЛА–САУ

где i_γ , i_β , χ_x , χ _y – коэффициенты законов управления САУ; , – аэродинамические коэффициенты ЛА.

В программе OTU угловые частоты собственных колебаний представлены аппроксима-ционными выражениями

Ω _х = Ω _{х 0} + (μ_х + η_х H)(q–1000); Ω _у = Ω _{у 0} + (μ _у + η _у H)(q –1000),

где Ω _{х 0} , Ω _{у 0}, μ_х , μ _у , η_х , η _у – константы.

Счисление пути ЛА в ортодромической системе координат производится с помощью уравнений навигации

= Vcos(ЗПУ–Ψ–β); Ż = Vsin(ЗПУ–Ψ–β). (15)

В программе OTU решение системы дифференциальных уравнений движения и навига-ции (11)–(15) производится методом Эйлера с шагом интегрирования h = 0,1 с.