Программирование сложных циклических процессов

Цель работы

Изучение приемов программирования сложных циклических процессов.

Методические указания

Как известно, любой циклический вычислительный процесс состоит из следующих частей:

- блока подготовки, в котором инициализируются начальные значения переменных, прежде всего параметра цикла;

- тела цикла, состоящего из операторов, которые выполняются до тех пор, пока выполняется условие продолжения цикла;

- блока или части, содержащей условие продолжения (окончания) циклического процесса.

Если телом цикла является циклическая структура, то такие циклы называются вложенными или сложными циклическими процессами.

Циклическая структура, содержащая в себе другую циклическую структуру, называется внешним циклом. А цикл, содержащийся внутри другого, называется внутренним.

Внутренний и внешний циклы могут быть любыми из трех рассмотренных выше типов: со счетчиком, с предусловием, с постусловием.

Правила организации как внешнего, так и внутреннего цикла такие же, как и для простых циклов, рассмотренных выше видов. Однако нужно выполнить следующее условие: все операторы внутреннего цикла должны полностью лежать в теле внешнего цикла.

Кроме того, нужно помнить, что при передаче управления от внешнего цикла к внутреннему, необходимо восстановить начальное значение параметра внутреннего цикла. В качестве примера рассмотрим фрагмент программы, который вычисляет значение функции двух переменных z = f(x, y), если аргумент x меняется от x0 до xN с шагом , а аргумент y меняется от y0 до . Блок-схема подобного вычислительного процесса представлена ниже.

Б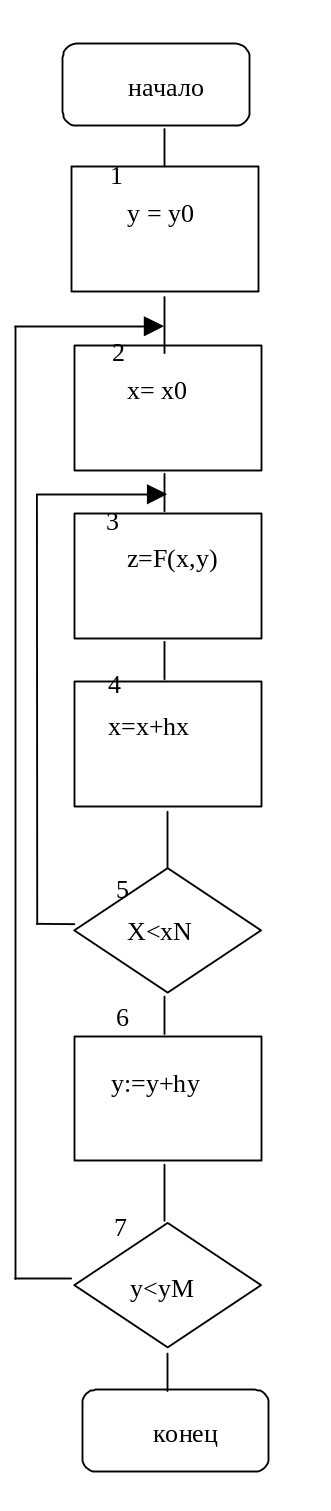 локи 3, 4, 5 составляют внутренний цикл с параметром x, внешний цикл

имеет параметр y и содержит блоки 2, 3, 4, 5, 6, 7. Ниже представлены варианты реализации представленного на рисунке двойного вложенного цикла.

Первый фрагмент программы использует оператор for и имеет вид:

..........

for (y0; y <= yM; y+ = hy)

{ printf ( y = %d, y);

for (x0; x <= xN; x + = hx)

{ z = F(x, y);

printf (x = %d _ _z = %d \n, x, z);

}

}

Второй вариант той же самой программы использует оператор do-while и имеет вид:

y = y0;

do

{ x = x0;

printf (y = %d, y);

do

{ z = F(x, y); printf (x = %d_z = %d \n, x, z);

x = x + hx;

}

while x  xN;

y = y + hx;

}

while y  xM;

Аналогично будет выглядеть вариант с использованием оператора while.

Пример выполнения задания

Вычислить значение интеграла методом трапеций для различных значений верхнего предела а, если он меняется от с шагом . Число точек разбиения интервала задано и равно n = 46. Для каждого вычисленного значения оценить абсолютную погрешность как разность между приближенным значением интеграла и точным, которая подсчитывается по первообразной интеграла.

Первообразная данного интеграла имеет вид: . Решение:

Формула трапеций для вычисления интеграла имеет вид или, в другом виде где y_k = y_i - значение подынтегральной функции в точке x_k = x_k-1 + h, где шаг . В программе можно использовать как первую, так и вторую функции.

Программа представляет сложный циклический процесс, в котором внешний цикл обеспечивает изменение верхнего предела интегрирования а с шагом в данном диапазоне, а внутренний цикл по переменной x обеспечивает вычисление интеграла при фиксированном значении а методом трапеций.

Необходимые пояснения к программе представлены в виде комментариев. Текст программы приведен ниже.

/* пример вычисления интеграла */

main ( )

{ float a, a0,aN, ha, x, x0, xN, hx, Jnt;

int n;

/* введем данные a0, aN, ha */

scanf (%f %f %f, &a0, &aN, &ha);

/* введем данные n */

scanf (%i , &n);

/*введем нижний предел интегрирования x0 */

scanf (%f , &x0);

/* начало цикла по а - верхнему пределу */

for (a = a0; a <= aN; a + = ha)

{ /* печатаем текущий верхний предел интегрирования */

printf (a = %f \n, a);

/* вычисляем интеграл при заданном а */

Jnt = 0; hx = (a - x0)/n;

for (x0; x <= a; x+ = h;

{

Jnt = Jnt + exp(-2*x);

}

Jnt = h*Jnt + h(exp(-2*x-) + exp(-2*a)/2;

/* печатаем а и значение Jnt */

printf (a = %d_ _Jnt = %d, a , Jnt

}

вставить оценку погрешности

}.

При выполнении варианта задания, в котором нужно найти корни уравнения f(x) = 0 при различных параметрах, прежде всего нужно представить уравнение в виде x = F(x), где F’(x) < 1. Это обеспечивает сходимость итерационного процесса.