
- •Проектирование программ простейшей структуры
- •Варианты заданий
- •Функции форматированного ввода и вывода
- •Задание к лабораторной работе
- •Разработка и реализация разветвляющихся алгоритмов
- •Программирование алгоритмов и программ циклической структуры при помощи цикла for
- •Контрольные вопросы
- •Варианты заданий
- •Программирование алгоритмов и программ циклической структуры с предусловием
- •Контрольные вопросы
- •Варианты заданий
- •Конструирование программ циклической структуры с постусловием
- •Контрольные вопросы
- •Варианты заданий
- •Программирование сложных циклических процессов
- •Контрольные вопросы
- •Варианты заданий
- •Программирование сложных циклических процессов
- •Контрольные вопросы
- •Варианты заданий
- •Обработка текста с использованием фунцкий ввода-вывода одного символа. Побитовые операции. Перключение ввода-вывода
- •Контрольные вопросы
- •Задания для выполнения
- •Варианты задания
Контрольные вопросы
Приведите синтаксическую структуру оператора DO-WHILE.
Чем отличается эта форма оператора цикла от ранее рассмотренных?
Как досрочно прервать выполнение циклического оператора DO-WHILE?
Что является телом в этом операторе цикла?
Когда выполняется проверка условия в этом цикле?
Что может использоваться в качестве условия? Приведите примеры.
Варианты заданий
1.Найти n,
при котором
![]() отличается от функции sh(x)
на величину 0.0001. Функция гиперболический
синус имеет вид:
отличается от функции sh(x)
на величину 0.0001. Функция гиперболический
синус имеет вид:
![]() .
.
Найти n, при котором
 отличается от функции сh(x)
на величину 0.001. Функция гиперболический
косинус имеет вид:
отличается от функции сh(x)
на величину 0.001. Функция гиперболический
косинус имеет вид:
 .
.Вычислить значение функции th(x) по формуле
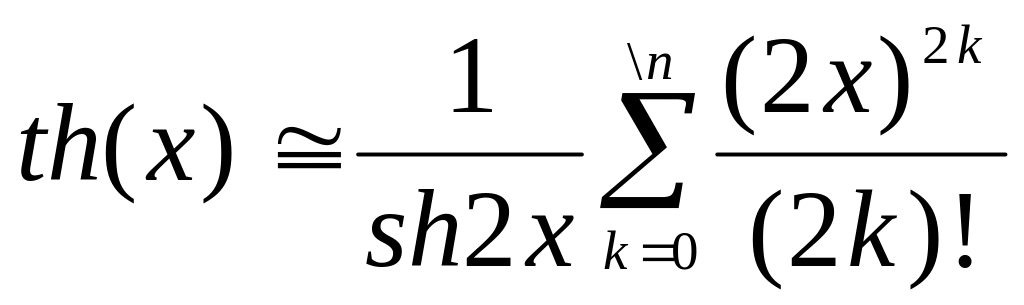 при n = 100 и найти абсолютную
погрешность вычисления th(x),
если
при n = 100 и найти абсолютную
погрешность вычисления th(x),
если
 ,
а
,
а

Вычислить значение функции
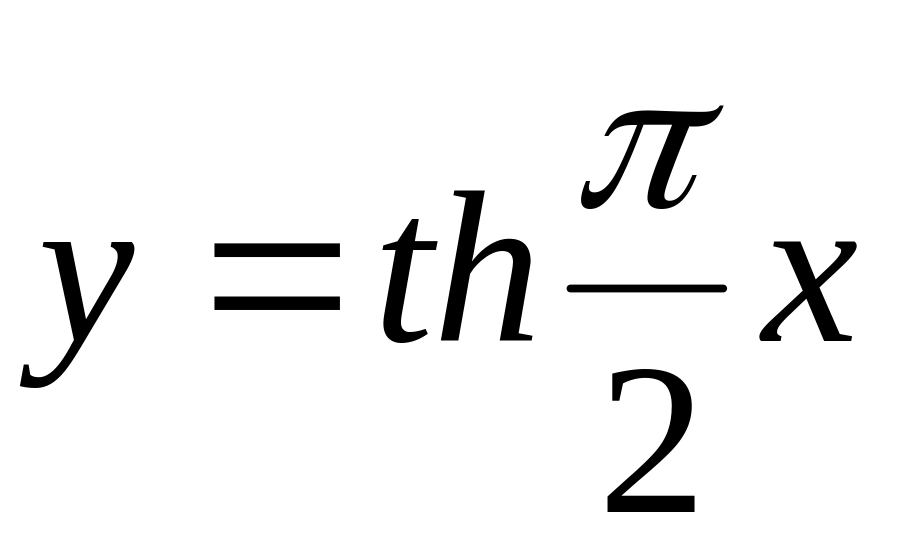 по формуле
по формуле
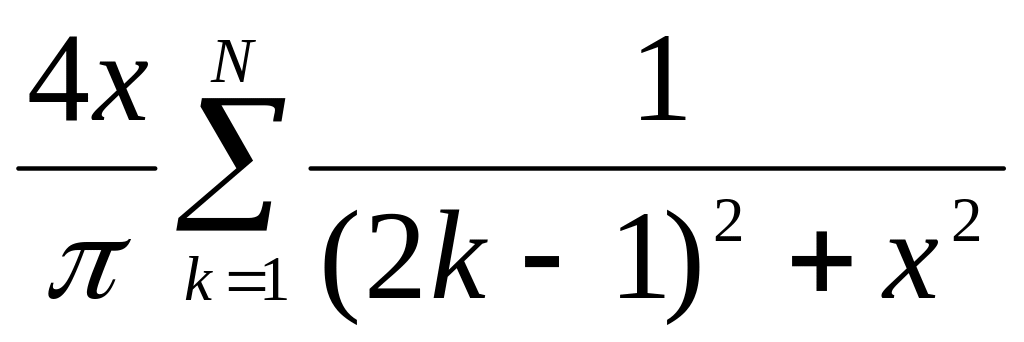 при N = 100. Вывести на экран
абсолютную погрешность вычисления.
при N = 100. Вывести на экран
абсолютную погрешность вычисления.Вычислить сумму
 для n = 40, x
= /2
и подсчитать абсолютную погрешность
для n = 40, x
= /2
и подсчитать абсолютную погрешность

Функция
 представляется суммой
представляется суммой
 .
Вычислить приближенное значение этой
функции для x = 0.2, n
= 20 и оценить абсолютную погрешность
вычисления.
.
Вычислить приближенное значение этой
функции для x = 0.2, n
= 20 и оценить абсолютную погрешность
вычисления.Функция
 представляется суммой
представляется суммой
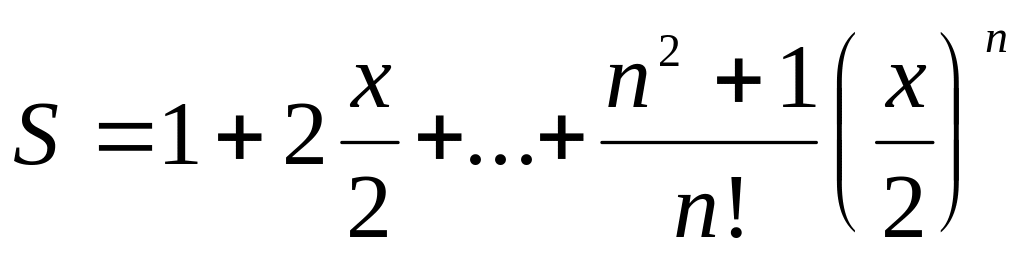 .
Вычислить значение этой функции для x
= 0.5, n = 30 и оценить абсолютную
погрешность вычисления.
.
Вычислить значение этой функции для x
= 0.5, n = 30 и оценить абсолютную
погрешность вычисления.Функция
 представляется суммой
представляется суммой
 .
Вычислить ее значение при x
= /5
и n = 40 и оценить абсолютную
погрешность вычисления.
.
Вычислить ее значение при x
= /5
и n = 40 и оценить абсолютную
погрешность вычисления.Вычислить значение
 и определить, будет ли вычисление
функции sh(x)
по данной формуле точнее, чем вычисление
по формуле, приведенной в п.1.
и определить, будет ли вычисление
функции sh(x)
по данной формуле точнее, чем вычисление
по формуле, приведенной в п.1.Вычислить значение
 и определить, будет ли вычисление
функции ch(x)
по данной формуле точнее, чем вычисление
по формуле, приведенной в п.2.
и определить, будет ли вычисление
функции ch(x)
по данной формуле точнее, чем вычисление
по формуле, приведенной в п.2.Функция может быть вычислена по формуле
 .
Определить, при каком N
совпадают значения функции, вычисленные
по первой и второй формулам.
.
Определить, при каком N
совпадают значения функции, вычисленные
по первой и второй формулам.Найти значения функции y = sh(x), используя рекуррентные соотношения

Найти значение функции y = ch(x), используя рекуррентные соотношения

Найти абсолютную погрешность вычисления функции y = sin(x) по приближенной формуле
 .
.Значение функции y = ln(x) может быть вычислено по рекуррентным выражениям вида:

Значение x 0 вводится с клавиатуры. Найти абсолютную погрешность вычисления y = ln(x) по рекуррентным соотношениям и непосредственно путем обращения к стандартной функции lnx.
Функция
 представляется
приближенно формулой
представляется
приближенно формулой
 .
Вычислить ее значение по первой и второй
формулам, взяв x = 0.2, n
= 100, и определить абсолютную погрешность
вычисления.
.
Вычислить ее значение по первой и второй
формулам, взяв x = 0.2, n
= 100, и определить абсолютную погрешность
вычисления.Функция y = sin(x) может быть вычислена с помощью рекуррентных соотношений
 Реализовать
программу вычислений y
= sin(x),
используя рекуррентные соотношения.
Определить абсолютную погрешность
вычисления при k = 100.
Реализовать
программу вычислений y
= sin(x),
используя рекуррентные соотношения.
Определить абсолютную погрешность
вычисления при k = 100.Вычислить точное значение функции
 ,
приближенное, используя представление
в виде суммы
,
приближенное, используя представление
в виде суммы
 и абсолютную погрешность.
и абсолютную погрешность.Функция y = arcsin(x) может быть представлена в виде суммы
 при x
< 1. Вычислить точное, приближенное
значение и абсолютную погрешность
вычисления по первой и второй формулам.
при x
< 1. Вычислить точное, приближенное
значение и абсолютную погрешность
вычисления по первой и второй формулам.Функция y = arctg(x) приближенно представляется суммой вида:
 при x
< 1. Вычислить значение функции по этой
формуле и оценить абсолютную погрешность.
при x
< 1. Вычислить значение функции по этой
формуле и оценить абсолютную погрешность.Функция arcsec(x) представляется суммой
 для x
> 1. Вычислить, насколько отличаются
друг от друга значения функции,
вычисленные при
для x
> 1. Вычислить, насколько отличаются
друг от друга значения функции,
вычисленные при

Вычислить значения гамма-функции Г(x) по приближенной формуле
 ,
где = 0.57722, для двух
значений
,
где = 0.57722, для двух
значений
 и оценить, насколько изменилось значение
функции при N2 = 200
по сравнению со значением при N1
= 100.
и оценить, насколько изменилось значение
функции при N2 = 200
по сравнению со значением при N1
= 100.Вычислить значение интегрального косинуса Ci(x) при x > 2 при двух значениях N = 50 и N = 100, если приближенно эта функция вычисляется по формуле
 .
.Вычислить значение интегрального синуса Si(x) по формуле
 при x
2 для двух значений N = 50
и N = 100 и вывести на экран
разность результатов этих двух
вычислений.
при x
2 для двух значений N = 50
и N = 100 и вывести на экран
разность результатов этих двух
вычислений.Вычислить значение интегрального косинуса Ci(x) по формуле
 ,
где x
2, = 0.57722, для N
= 50 и N = 100 и оценить разность
этих двух вычислений.
,
где x
2, = 0.57722, для N
= 50 и N = 100 и оценить разность
этих двух вычислений.
Лабораторная работа № 7
