1.2.4. Механизмы генерации и потерь

Большая часть примеси существовует в кремнии в более чем одном состоянии, особенно при высоких уровнях концентрации. Одним из типичных состояний является состояние замещения с большой подвижностью, в то время как другие состояния, если они имеются, могут образовывать прецепитат или кластер, которые менее подвижны. Обмен между этими двумя состояниями описывается членами генерации и потерь в уравнения непрерывности (1.8) для подвижных примесей. В SUPREM II включена модель, описывающая кластеризацию мышьяка [41, 42]. Из-за отсутствия необходимых моделей влиянием кластеризации и преципитации на диффузию других примесей можно пренебречь. Химическая реакция для мышьяка имеет вид

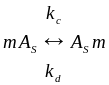, (1.30)

где m - число атомов в кластере, а k_c и k_d - коэффициенты кластеризации и декластеризации. Концентрация атомов в кластерах C_c определяется следующим образом

, (1.31)

где C_T - полная концентрация, а С - концентрация мышьяка в состоянии замещения. Уравнение сохранения для C_C может быть записано в следующем виде

, (1.32)

где l и g относятся к членам, описывающим генерацию и потери в уравнении (1.8).

Таким образом, определяя равновесный коэффициент кластеризации k_e как

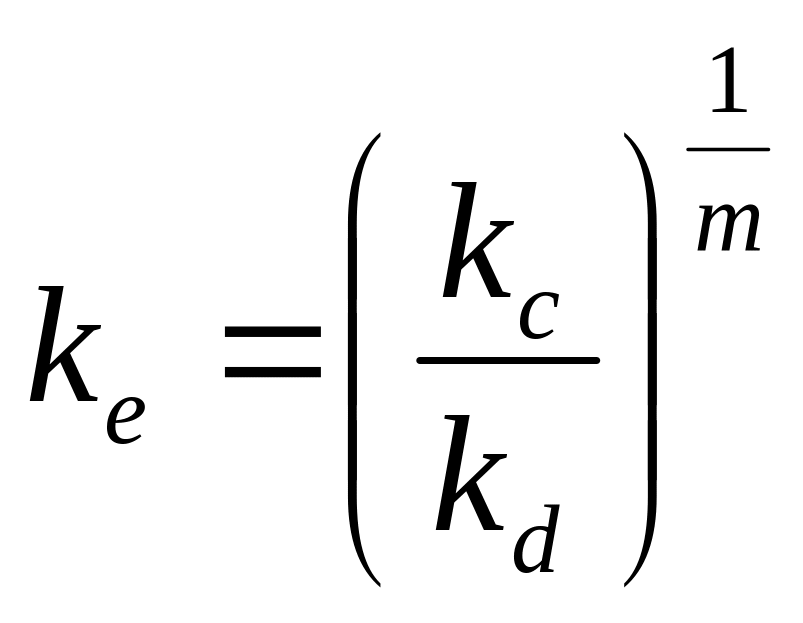, (1.33)

можно переписать уравнение (1.32) в следующей форме

. (1.34)

Уравнение (1.34) вместе с уравнением (1.8) используются для описания термической миграции атомов мышьяка в кремнии. Размер кластера m, который лучше всего удовлетворяет экспериментальным данным, равен 4. Однако кластеры могут существовать и в более крупных размерах. Скорость декластеризации k_d рассмотрена в работе [41]. В равновесном состоянии (при dC_C/dt = 0) уравнение (1.34) имеет вид

. (1.35)

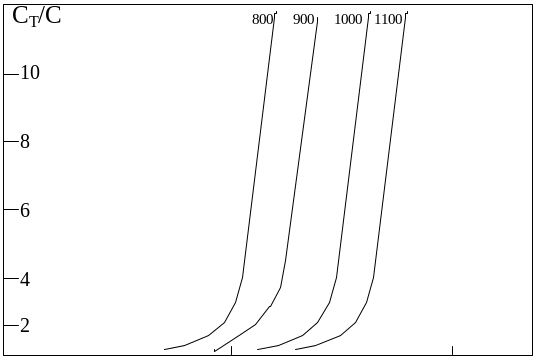
Это условие иллюстрируется рис.1.8. Видно, что кластеризация налагает ограничение на максимум концентрации атомов замещения и, следовательно, на количество электрически активных атомов мышьяка.

Хотя модель кластеризации предсказывает формирование и растворение кластеров в процессе загонки и последующей разгонки мышьяка, следует учесть и концентрацию кластеров после имплантации мышьяка. В этом случае произвольно полагается, что начальный профиль атомов мышьяка в кластерах представляет собой просто профиль, определяемый термическим равновесием при температуре отжига и задаваемым имплантационным профилем.

1.3. Термическое окисление

Скорость роста SiO₂ на кремнии в программе SUPREM II описывается хорошо известной формулой [43]

, (1.36)

где Z_ox - толщина окисной пленки; t - длительность процесса окисления, a A и B - параметры, которые связываются с коэффициентами линейного и параболического роста K_P и K_L и с парциальным давлением P_O2 кислорода посредством соотношений

,

.

Параметр  определяется через начальную толщину окисла выражением

. (1.37)

При относительно низкой концентрации примесей K_P и K_L зависят только от ориентации кристалла кремния и окислительной cреды и являются функцией температуры.

Хорошо известно, что при высоких уровнях поверхностной концентрации примесей (в областях истока и стока МОП - транзистора и в области эмиттера биполярного транзистора) скорость окисления кремния повышается. Более детальное описание этого явления дается в работе [44]. Было обнаружено, что линейный коэффициент скорости роста окисла существенно увеличивается, что отражается на повышении скорости реакции, тогда как коэффициент скорости роста, который зависит от диффузии кислорода в оксиде кремния, повышается незначительно. Такое усиление скорости роста уменьшается с повышением температуры. В SUPREM II используется модель, предложенная в работе [45], которая количественно связывает коэффициенты ускорения для K_P и K_L с поверхностной концентрацией примеси. Основная идея заключается в том, что скорость окисления кремния зависит от концентрации вакансий в кристаллической решетке, которая, в свою очередь, зависит от присутствия примесных атомов.

Линейный коэффициент скорости роста окисла может быть записан следующим образом

, (1.38)

где K_Lⁱ – собственный коэффициент (то есть при низкой концентрации примеси),  - эмпирический параметр, получаемый из выражения

. (1.39)

С^T - нормализованная полная концентрация вакансий:

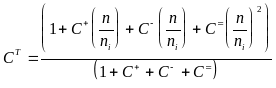(1.40)

при , E_d⁺ = 0.35 eV;

, E^--= E_g - 0.57 eV;

, E⁼ = E_g - 0.11 eV.

Эти выражения cледует рассматривать как нормализованные собственные концентрации вакансий в трех зарядовых состояниях с соответствующими энергетическими состояниями в кремниевой подложке. Ширина запрещенной зоны кремния E_g и собственный уровень E_i получаются как функции температуры из выражений

, eV, (1.41)

.

10²⁰ 10²¹ см^-3

Рис.1.8. Зависимость нормализированной полной концентрации атомов

мышьяка от концентрации атомов мышьяка в состоянии замещения

при термическом равновесии. Результаты расчетов получены по модели кластерообразования. Параметр - температура процесса в град. Цельсия

Для n-типа примесей увеличение параболического коэффициента скорости окисления также было получено в работе [45]. При этом

, (1.42)

где , (1.43)

K_Pⁱ - собственный коэффициент параболической скорости, а С_T - полная концентрация атомов примеси n-типа.

Поскольку при окислении поверхностная концентрация примеси изменяется благодаря диффузионному и сегрегационному перераспределениям, рассчитанные коэффициенты K_L и K_P могут, вообще говоря, зависеть от времени. В программе SUPREM II, в отличие классического уравнения скорости роста (1.36), где используется то же уравнение в форме приращения

. (1.44)

Таким образом, при моделировании процесса окисления с перераспределением примесей (при достаточно малом временном шаге t) коэффициенты А и В рассчитываются из поверхностных концентраций примеси на каждом временном шаге и затем вычисляются соответствующие приращения окисной пленки Z_ox.