Система уравнений предиктора

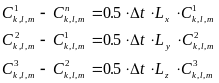(4.8)

решается методом прогонки.

Далее по явной схеме

(4.9)

осуществляется коррекция полученных результатов. На каждом временном интервале проводится итерационное уточнение коэффициентов диффузии.

Для расчета коэффициента диффузии D используется, как и в программе SUPREM II, вакансионная модель.

Введение фиктивной области над подложкой позволяет осуществлять моделирование перераспределения примеси для областей подложки и окисла по единой численной схеме. Различия между окислом и подложкой учитываются при расчете коэффициента диффузии. Такой подход требует увеличения количества узлов сетки, однако при этом вычислительный алгоритм существенно упрощается, так как исчезает необходимость перестраивать пространственную сетку на каждом временном шаге.

Задача решается в прямоугольной области , где X, Y, Z выбирааются такими, чтобы значение концентрации C(x,y,x) на границах практически не изменялось. Область  включает фиктивные узлы, в которых полагается C=0. На границе области задается условие симметрии (n - внешняя нормаль). Размер фиктивной области выбирается исходя из предполагаемой толщины окисла, который рассчитывается в приближении модели [29]:

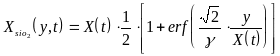, (4.10)

, (4.11)

.

Типичный результат двумерного расчета толщины окисной пленки при высокотемпературном окислении представлен на рис. 4.2.

Диффузионный процесс перераспределения примеси происходит неравномерно во времени. Вначале он протекает, как правило, быстрее, а затем замедляется. В связи с этим целесообразно введение переменного шага по времени. Изменение временного шага в зависимости от количества итераций на предыдущем временном шаге осуществляется по методике, описанной в работе [34].

Такой подход позволяет значительно повысить адаптивность метода, поскольку допустимый размер временного шага существенно зависит от таких параметров, как тип примеси, температура отжига, доза имплантации и т.д.

Рис. 4.2. Результат двумерного моделирования роста окисла

X_o = 10Å; = 1; B = 3.92·10⁴ Å ²/мин; B/A=46.3 Å/мин; T=1100^oC; t=60 мин;

парциальное давление кислорода = 10⁵ Па;

координаты x и y – в ангстремах

4.3. Программная реализация

Приведенная численная схема реализована на языке С (стандарт ANSI), что решает проблему переноса математической части программы на различные аппаратные платформы. Использовалась операционная среда Windows NT, поскольку она универсальна по отношению к аппаратным платформам. Интерфейсная часть программы реализована посредством использования системы визуального программирования Delphi.

4.4. Иллюстрация типичных результатов трехмерных расчетов

На рис. 4.3 приведены результаты трехмерного моделирования перераспределения ионно-имплантированного фосфора в кремниевой подложке в результате высокотемпературного окисления.

б)

а)

y

y

в)

г)

x

x

Рис. 4.3. Результаты трехмерного расчета профиля распределения фосфора в кремниевой подложке в результате имплантации (а, в)

и отжига в окислительной среде (б, г);

а и б – двумерные профили в сечении Z = 0; в и г – изоконцентрические линии;

(в: 1 – C = 8.4·10¹⁹ см^-3; 2 - C = 1.9·10¹⁸ см^-3; 3 - C = 4.1·10¹⁶ см^-3;

4 - C = 9.2·10¹⁴ см^-3; 5 - C = 2.0·10¹³ см^-3; 6 - C = 4.5·10¹¹ см^-3);

(г: 1 – C = 1.5·10¹⁸ см^-3 ; 2 - C = 3.5·10¹⁶ см^-3; 3 - C = 8.1·10¹⁴ см^-3;

4 - C = 1.9·10¹³ см^-3; 5 - C = 4.3·10¹¹ см^-3);

по осям координат представлены: концентрация С в см^-3; координаты Х и Y в мкм

Параметры имплантации представленных результатов следующие: энергия имплантируемых ионов E = 100 кэВ; доза Q = 10¹⁵ см^-2, размер маски 1x1 мкм. Параметры отжига: температура T = 1020^oC, длительность t = 60 мин, среда - сухой кислород. Расчетная сетка имела размеры 50х50х50. Результаты моделирования приведены для сечения Z = 0.