4. Многомерное моделирование технологии формирования ис

В данном разделе кратко описываются основные особенности многомерного (2D и 3D) моделирования имплантационного легирования и высокотемпературного окисления, изложенные в работах [47-50].

4.1. Моделирование профиля имплантированных примесей

Послеимплантационное трехмерное пространственное распределение примеси F(x,y,z) моделируется посредством использования интеграла статистической функции распределения по переменным , 

, (4.1)

где .

Здесь , - функции распределения Гаусса с переменной по глубине дисперсией

. (4.2)

Дисперсия распределения определяется формулой

. (4.3)

Функция распределения Pearson-IV P(x) строится таким же образом, как и в программе SUPREM II (выражение (1.6)).

Дисперсия распределения в поперечном направлении должна быть положительной, поэтому необходимо выполнение условий

. (4.4)

Неравенства (4.4) ограничивают применимость модели в случае имплантации очень медленных тяжелых ионов (E<1 кэВ), когда х<<Rp, а также для легких ионов на больших глубинах, где функция P(x) принимает низкие значения. Это позволяет полагать F(x,y,z)=0 в области, где неравенства эти неравенства не удовлетворяются.

4.2. Моделирование перераспределения примеси в процессе окисления

В общем случае перераспределение примеси при термическом окислении описывается нелинейным диффузионным уравнением

. (4.5)

В начальный момент времени t=0 C(x,y,z)=F(x,y,z).

Нелинейность уравнения (4.5) обусловлена существенной зависимостью коэффициента диффузии D от концентрации C.

На рис. 4.1 показана система координат, используемая при трехмерном моделировании диффузионного перераспределения примесей, а также характерные точки пространственной сетки. Начало координат находится на поверхности, в центре окна; координата Х направлена вглубь образца перпендикулярно поверхности моделируемой области.

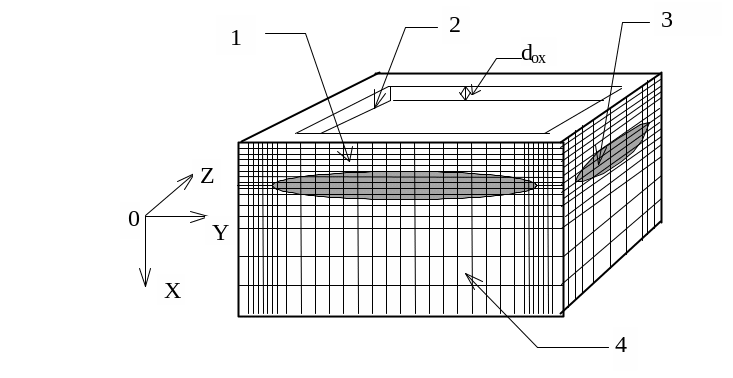
Рис. 4.1. Система координат, используемая при численном решении

нелинейного уравнения диффузии (4.5):

1 – фиктивная область; 2 – окно в маске;

3 – окисел; 4 – подложка; d_ox – толщина окисла

Уравнение (4.5) решается численно методом конечных разностей в отличие от традиционно используемого метода конечных элементов. Для удобства и большей наглядности методики построения численного алгоритма целесообразно его представить в операторном виде:

. (4.6)

где , , .

Дифференциальные операторы аппроксимируются конечно-разностными соотношениями вида

, (4.7)

где , ,

, .

Тогда .

Аналогично аппроксимируются дифференциальные операторы L_yС и L_zС.

Для решения диффузионного уравнения (4.5) используется метод “предиктор – корректор“. На этапе предиктора рассчитываются концентрации примесей C(x,y,z) в узлах сетки по неявной схеме без учета зависимости потока от пространственных направлений (X,Y,Z). На этапе корректора концентрации в узлах сетки рассчитываются по явной схеме на основании результатов, полученных на этапе предиктора.