Ш. Хиральность. Молекулы с одним асимметрическим атомом.
Явление структурной изомерии, столь типичное для органической химии, обусловлено различным порядком связи атомов в молекулах изомеров:
CH3-CН2-OH этанол |
CH3-CН2-CН2- CH3 бутан |
CН2=СН-СН2-СН3 бутен-1 |
CH3-О-CH3 диметиловый эфир |
CH3-CH(CH3)-CH3 изобутан |
CH3-CH=CH-CH3 бутен-2 |
Помимо структурных изомеров, существуют также изомеры, порядок связи атомов в молекулах которых одинаков, но различно расположение атомов в пространстве. Их называют пространственными изомерами, или стереоизомерами (либо стереомерами). Эти изомеры подразделяются на два класса: энантиомеры и диастереомеры. Отнесение стереоизомеров к одному из этих двух классов основано на том, возможно, или невозможно превратить один изомер в другой путём отражения в зеркальной плоскости (разумеется, речь идет о формальной процедуре, а не о каком-то реальном процессе).
Прежде, чем обсуждать упомянутые изомеры, рассмотрим соотношения между объектом и его зеркальным отображением на примере, не относящемся к химии.
Допустим, у нас имеется чашка, на которой нет каких-либо рисунков. Сравним эту чашку (А) с ее отображением в зеркале (А').
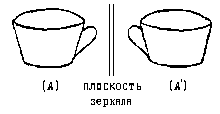
Попробуем мысленно совместить зеркальное отображение чашки c оригиналом так, чтобы они полностью совпали. В данном случае это возможно. Нанесем на одну сторону чашки рисунок и вновь сравним чашку (Б) с ее зеркальным отображением (Б')
Теперь совместить нашу "меченую" чашку с ее отображением в зеркале не удастся. Например, если совместить эти чашки так, чтобы совпали ручки, то рисунки окажутся по разные стороны, и наоборот.
Аналогично, нельзя совместить ладони левой и правой рук. В то же время, если мы посмотрим на отражение левой ладони в зеркале, то увидим правую ладонь.
Объект, не совместимый со своим зеркальным отображением, называется ХИРАЛЬНЫМ. |
Термины "хиральный" и "хиральность" происходят от греческого слова "cheir" - рука.
Как определить, хирален объект или нет, не прибегая к помощи зеркала? Для этого надо проверить наличие элементов симметрии у данного объекта. Если в объекте присутствует хотя бы один элемент симметрии группы зеркально-поворотных осей (Sn), хиральность невозможна.
ЭЛЕМЕНТЫ СИММЕТРИИ, ИСКЛЮЧАЮЩИЕ ХИРАЛЬНОСТЬ: плоскость симметрии ( ) центр симметрии (L) зеркально-поворотные оси высших порядков (Sn, n>2) |
Если у объекта нет перечисленных элементов симметрии, такой объект обязательно хирален, то есть несовместим со своим зеркальным отображением. Так, в рассмотренном выше примере у чашки (А) имеется плоскость симметрии, проходящая через ручку и рассекающая чашку пополам. В чашках (Б) и (Б') отсутствует плоскость симметрии (как и другие элементы симметрии группы Sn), поскольку рисунок находится лишь на одной стороне чашки.
Хиральный объект на первый взгляд можно было бы назвать асимметричным. Однако, это не совсем верно. Понятие "асимметричный" подразумевает отсутствие всех элементов симметрии, за исключением тривиального С1. В хиральном же объекте могут присутствовать простые поворотные оси Сn, n> I