В.П.Дядченко "Введение в стереохимию"

Современная органическая химия  немыслима   без представлений о пространственном строении молекул и его влиянии на ход химических реакций, что составляет предмет стереохимии. В стереохимии используются определенные способы изображения молекул, а также стереохимическая номенклатура. Цель настоящего пособия - познакомить читателя с основными понятиями, которыми оперирует стереохимия.  Элементарные сведения по стереохимии изложены в разделах  I-IX. В разделе X помещен дополнительный материал,  знание которого также поможет успешному изучению курса органической химии.

I. Элементы симметрии.

Для описания пространственного строения молекул важно знание элементов симметрии. Термин "симметрия" интуитивно понятен. Обычно это слово ассоциируется с ограненным камнем, архитектурным сооружением и т.п. Симметричный объект содержит один или несколько элементов симметрии, для которых  можно дать строгое математическое определение. Ниже приведены простейшие сведения об элементах симметрии.

Центр симметрии (центр инверсии),I

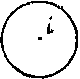
Центром симметрии объекта называется точка   i , удовлетворяющая следующим условиям. Для любой точки А, принадлежащей объекту, всегда найдется точка А', также принадлежащая данному объекту такая, что:

а)точки А, i , А'  лежат на одной прямой;

б)точки А и А'  равноудалены от точки   i .

Примеры центрально-симметричных объектов:

квадрат	правильный шестиугольник	круг

Плоскость симметрии

Плоскостью симметрии называется плоскость   удовлетворяющая следующим условиям. Для любой точки А, принадлежащей  объекту, всегда найдется точка А, также принадлежащая этому объекту такая, что:

а)прямая, проведенная через точки А и А', перпендикулярна плоскости   ;

б)точки А и А' равноудалены от плоскости  ,

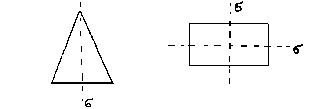
равнобедренный треугольник     прямоугольник

(плоскости симметрии   перпендикулярны плоскости чертежа и пересекают ее по пунктирным линиям)

Простая ось симметрии n-го порядка Cn

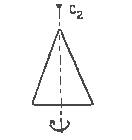
Осью симметрии  n-ного порядка называется ось, проходящая через данный объект, при повороте вокруг которой на угол 360°/n  объект совмещается сам с собой.

равнобедренный треугольник: ось симметрии С2	правильный шестиугольник : показаны две оси С2, лежащие в  плоскости чертежа; ось С6 перпендикулярна плоскости чертежа

Ось Симметрии С₁ (поворот на 360°) называется тривиальным элементом симметрии. Существует также ось симметрии бесконечного порядка С . Поворот вокруг этой оси на любой угол приводит к coвмещению объекта  с самим собой (ось, проходящая через центр круга и  перпендикулярная  его плоскости; любая ось, проходящая через центр   шара).

Зеркально-поворотная ось симметрии n - ого порядка Sn.

Это сложный элемент симметрии, включающий две операции: поворот вокруг оси на угол 360°/n   и отражение в плоскости, перпендикулярной данной оси. При выполнении операций, соответствующих оси   Sn, объект совмещается сам с собой.

Примером объекта, в котором имеется зеркально-поворотная ось, может служить деревянный квадрат, по углам которого вбиты четыре гвоздя: два сверху и два снизу.

Ось  S₄ перпендикулярна плоскости квадрата и проходит через его центр. Одного поворота вокруг оси   S₄ на 90° недостаточно, чтобы данный объект совпал сам с собой. Для этого необходимо последующее отражение в плоскости, перпендикулярной оси  S₄ и рассекающей квадрат пополам (нижняя часть квадрата при отражении переходит вверх, верхняя - вниз);

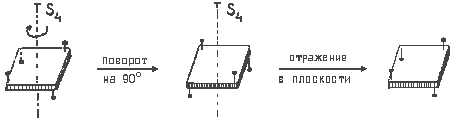
Помимо оси  S₄ в данном объекте присутствует также простая поворотная ось C₂ (поворот на 180°), совпадающая с осью   S₄. Следует заметить, что плоскость симметрии эквивалентна зеркально-поворотной оси первого порядка (поворот на 360° и отражение в плоскости );          ,

Аналогично, центр симметрии эквивалентен оси симметрии  S₂(поворот на 180⁰ и отражение в плоскости, перпендикулярной оси): Таким образом, элементы симметрии   составляют группу зеркально-поворотных осей.