
- •Порядок выполнения контрольных работ
- •Тема 1. Растяжение-сжатие Задача 1.1. Расчет стержня
- •Задача 1.2. Расчет статически-неопределимого стержня
- •Задача 1.3. Расчет статически-неопределимой шарнирно-стержневой системы
- •Тема 2. Кручение Задача 2.1. Расчет вала
- •Задача 2.2. Расчет статически-неопределимого вала
- •Тема 3. Сдвиг (срез) Задача 3.1. Расчет заклепочного соединения
- •Тема 4. Изгиб Задача 4.1. Расчет балки
- •Задача 4.2. Расчет балки несимметричного сечения
- •Задача 4.3. Расчет статический-неопределимой балки
- •Тема 5. Сложное сопротивление Задача 5.1. Косой изгиб
- •Задача 5.2. Внецентренное растяжение (сжатие)
- •Задача 5.3. Изгиб с кручением
- •Тема 6. Напряженное состояние Задача 6.1. Плоское напряженное состояние
- •Некоторые механические характеристики материалов
- •Список рекомендуемой литературы
- •Содержание
Задача 4.2. Расчет балки несимметричного сечения
Условие
задачи: На горизонтально расположенную
балку, жестко закрепленную одним концом,
действуют активные нагрузки
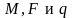 .
Сечение стержня несимметрично, материал
имеет различные прочностные свойства
при растяжении и сжатии.
.
Сечение стержня несимметрично, материал
имеет различные прочностные свойства
при растяжении и сжатии.
Требуется: Построить эпюры поперечных сил и изгибающих моментов и подобрать сечение балки из расчета на прочность.
Исходные данные к задаче 4.2
Таблица 4.2
Данные |
Нагрузки |
Координаты |
а, м |
Сечение (рис.4.2.1) |
||||||
|
|
|
|
|
нач. |
кон. |
||||
0 |
-15 |
20 |
10 |
3a |
4a |
a |
3a |
0,5 |
3 |
|
1 |
20 |
15 |
-15 |
a |
2a |
0 |
2a |
1,3 |
2 |
|
2 |
-10 |
-30 |
20 |
1,5a |
2,5a |
a |
2a |
1,1 |
5 |
|
3 |
15 |
20 |
-20 |
a |
3,5a |
0 |
a |
0,6 |
1 |
|
4 |
-10 |
-15 |
-10 |
3a |
2a |
2a |
4a |
0,8 |
3 |
|
5 |
15 |
-25 |
15 |
a |
4a |
0 |
2a |
1,4 |
4 |
|
6 |
-20 |
15 |
10 |
1,5a |
2,5a |
a |
2a |
1,0 |
2 |
|
7 |
15 |
30 |
-20 |
a |
4a |
0 |
a |
1,2 |
1 |
|
8 |
-20 |
-20 |
10 |
3a |
3,5a |
2a |
4a |
0,7 |
5 |
|
9 |
10 |
25 |
-15 |
1,5a |
2a |
a |
3a |
0,9 |
4 |
|
Пр. |
15 |
-15 |
20 |
3a |
4a |
0 |
2a |
1,0 |
6 |
|
Вар |
II |
I |
III |
III |
I |
II |
II |
I |
III |
|
Указания:.
Допускаемые напряжения
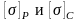 возьмите
из табл. 5.2. Жесткую заделку расположите
на левом конце балки, там же выберите
начало координат. На соответствующих
координатах расположите внешние
нагрузки, в соответствии с которыми
разобьете балку на силовые участки.
Длину каждого участка обозначьте через
.
возьмите
из табл. 5.2. Жесткую заделку расположите
на левом конце балки, там же выберите
начало координат. На соответствующих
координатах расположите внешние
нагрузки, в соответствии с которыми
разобьете балку на силовые участки.
Длину каждого участка обозначьте через
.
В нашем примере три силовых участка.

Рис.4.2.1.
Решение: Составим уравнения внутренних усилий для каждого силового участка балки и построим эпюры, изображенные на рис. 4.2.2. Пример построения эпюр дан в предыдущей задаче.
По
эпюре
определяем опасное сечение балки, где
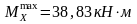 (по
абсолютной величине). Размер сечения
вычисляем из условия прочности при
изгибе по осевому моменту сопротивления
сечения, причем отдельно делаем расчет
по растянутым волокнам и отдельно – по
сжатым.
(по
абсолютной величине). Размер сечения
вычисляем из условия прочности при
изгибе по осевому моменту сопротивления
сечения, причем отдельно делаем расчет
по растянутым волокнам и отдельно – по
сжатым.
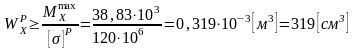
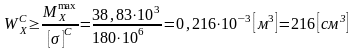

Рис. 4.2.2.
Теперь
определим геометрические характеристики
сечения
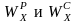 .
.
Прежде
всего, следует определить положение
центра тяжести сечения, т.к. через него
проходит нейтральная линия. Найдем его
по формуле
 ,
,
где
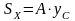 -
статический момент, а
-
статический момент, а
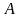 -
площадь сечения.
-
площадь сечения.
Данное сечение можно представить в виде двух фигур:
1 –
прямоугольник 3bx5b; 2 – прямоугольный
вырез (т.е. отрицательная фигура) 2bx2b.
Координаты
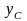 будем откладывать от оси
будем откладывать от оси
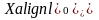 (см. рис. 4.2.3.).
(см. рис. 4.2.3.).
Тогда
 .
.
Проведем
через центр тяжести ось
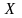 и построим эпюры нормальных напряжений
.
В данном случае сечение расположено
нерационально, т.к.
и построим эпюры нормальных напряжений
.
В данном случае сечение расположено
нерационально, т.к.
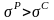 ,
что не согласуется с исходными данными,
по которым
,
что не согласуется с исходными данными,
по которым
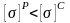 .
В таком случае сечение переворачиваем
(см. рис. 4.2.4).
.
В таком случае сечение переворачиваем
(см. рис. 4.2.4).
Определим осевой момент инерции сечения
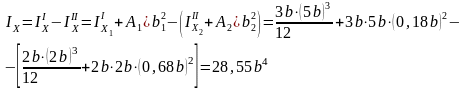 Теперь
определим осевые моменты сопротивления
сечения и для растянутых и для сжатых
волокон:
Теперь
определим осевые моменты сопротивления
сечения и для растянутых и для сжатых
волокон:
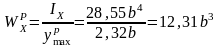 ,
,
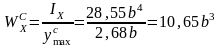 .
.
Подберем размеры сечения:
по растянутым волокнам
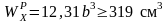 ,
откуда
,
откуда
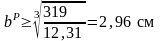 ;
;
по сжатым волокнам
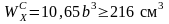 ,
откуда
,
откуда
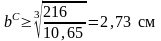 .
.
Выбираем
большее значение и принимаем
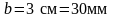 .
.

Рис.4.2.3.

Рис. 4.2.4.
