Раздел 8 Расчет динамических параметров системы

Определим передаточную функцию всей системы по заданным передаточным функциям датчика, регулятора, исполнительного механизма и объекта регулирования.

Передаточная функция объекта регулирования: W_о.р.(p) =

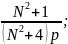
Передаточная функция датчика: W(p) =

Передаточная функция регулятора: W(p) =

Передаточная функция исполнительного механизма: W(p) =

Передаточная функция объекта регулирования определяется выражением:

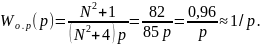
Передаточная функция датчика:

Передаточная функция регулятора:

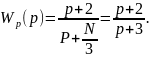
Передаточная функция исполнительного механизма:

Для определения передаточной функции обратной связи необходимо воспользоваться формулой

Подставив выражение передаточной функции в эту формулу, получим

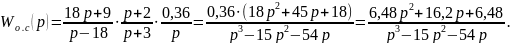
Для определения передаточной функции системы необходимо воспользоваться формулой:

Подставим в это выражение полученные, передаточные функции и получим результирующее выражение передаточной функции системы:

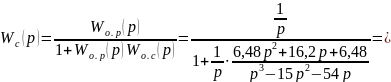
Итак, передаточная функция описывается выражением

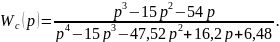
Для нахождения временной функции переходного процесса упростим выражение, описывающее передаточную функцию. Исключим в числителе , а в знаменателе . Для дальнейшего исследования функция будет иметь вид

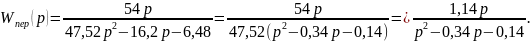
Для определения переходной функции представим общее выражение в виде двух слагаемых, которые можно получить, определив корни характеристического уравнения

где p₁ и p₂ – значения корней характеристического уравнения.

Для определения корней характеристического уравнения приравняем к нулю знаменатель:

Найдем дискриминант уравнения

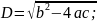
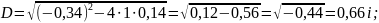
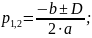
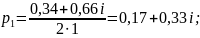
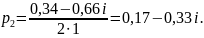
Подставим значения характеристического уравнения p₁ и p₂ в выражение W_пер (p) и таким образом определим коэффициенты А и B:

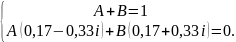
Подставляем А=1-B во второе уравнение и решим относительно B:

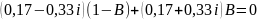
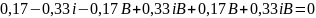
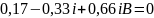
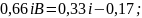
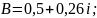
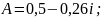
Для определения функций времени необходимо воспользоваться обратным преобразованием Лапласа:

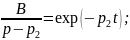
Далее определяем переходную функцию системы, которая определяется выражением

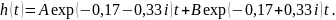
Преобразуем это выражение

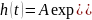
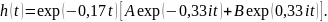
Подставим значения A и B:

или

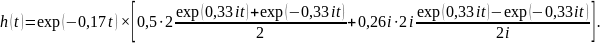
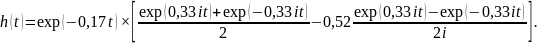
В результате получим

.

Две гармонические функции можно заменить одной, если определить модуль и фазу результирующего колебания.

Определим модуль a=1; b=-0,52; М=(a²+b²)^1/2=1

-31°.

В результате получим выражение

Переведем величину угла в градусах в радианы и получим

или

Рисунок 11 - График функции переходной

Построение графика данной функции осуществили с учетом того, что

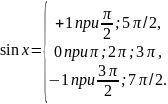
В нашем случае согласно построенному графику время регулирования t_рег=8.

Раздел 9 Устойчивость системы

Устойчивость системы – это свойство возвращаться к состоянию установившегося равновесия, после устранения возмущения, нарушившего равновесие.

Устойчивость является необходимым условием работоспособности системы.

Система неустойчива, если после снятия возмущения выходная величина неограниченно удаляется от первоначально установившегося режима.

Если график переходного процесса сходящийся, то система устойчива, а если расходящийся то система неустойчива.

Устойчивость системы характеризуется ее свободными движениями. Свободные движения системы описываются однородными дифференциальными уравнениями, т.е. уравнениями без правой части. Для определения устойчивости системы исследуется уравнение. Встречаются различные комбинации корней.

Если характеристическое уравнение имеет только вещественные и неравные корни, то с течением времени система будет удаляться от положения равновесия, т.е. будет неустойчивой.

Если характеристическое уравнение имеет пару комплексных сопряженных корней, то процесс будет затухать. При наличии пары чисто мнимых корней в системе возникают незатухающие гармонические колебания, система находится на границе устойчивости.

Если характеристическое уравнение имеет один нулевой корень, а все остальные корни вещественные и отрицательные, то система имеет множество состояний равновесия.

Для устойчивости необходимо, чтобы все вещественные корни характеристического уравнения были отрицательны, а комплексные корни имели отрицательную вещественную часть.

Определим амплитудно-частотные характеристики звеньев и системы в целом. Передаточная функция объекта регулирования определяется выражением

Для определения частотной характеристики объекта регулирования произведем замену в передаточной функции объекта

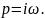
Получим частотную характеристику объекта регулирования (рисунок 10)

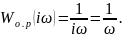
Рисунок 12 - Характеристика частотная объекта регулирования

Определим частотную функцию датчика

Для выделения действительного и мнимого значений умножаем числитель и знаменатель на комплексно-сопряженное значение знаменателя:

Далее определим модуль, полагая, что

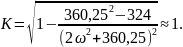
Построим график с учетом выражения

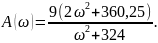
Рисунок 13 - Функция частотная датчика

Определим спектральную характеристику исполнительного механизма

Произведем замену в передаточной функции исполнительного механизма

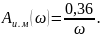
Рисунок 14 - Характеристика спектральная исполнительного механизма

Определим спектральную характеристику регулятора.

Передаточная функция имеет вид

Приме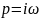м и получим

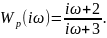
Для выделения действительного и мнимого значений умножаем числитель и знаменатель на комплексно-сопряженное значение знаменателя:

Выделим действительную и мнимую части:

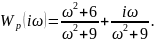
Определим модуль, полагая, что

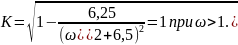
Построим график с учетом выражения

Рисунок 15 - Характеристика спектральная регулятора

Определим частотную характеристику обратной связи – ДРИМ.

Имеем передаточную функцию

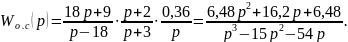
Рисунок 16 – Характеристика частотная обратной связи – ДРИМ

Частотную характеристику всей системы можно записать выражением

Устойчивость системы определим по положению корней p₁ и p₂ из уравнения

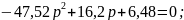
По критерию Ляпунова, если характеристическое уравнение имеет пару комплексных сопряженных корней, то процесс будет затухать. Следовательно, наша система не устойчива.