5.1 Статические характеристики устройств системы и цепи обратной связи

Различают два основных режима работы САУ:

1. Статический (установившийся), при котором каждое последующее звено системы не должно влиять при выходе на информацию предыдущего. Так как в системе автоматического управления каждое последующее аналоговое устройство является нагрузкой для предыдущего.

2. Динамический, при котором входная и выходная величины переходят из одного установившегося значения в другое, тем самым изменяются во времени.

Статической характеристикой элемента САУ называют график, показывающий зависимость установившегося значения выходной величины к значению входной.

Статическая характеристика объекта регулирования описывается уравнением:

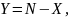
где N=9.

Для построения характеристики возьмем следующие значения:

Xд	0	1	2	3
Yд	9	8	7	6

По этим значениям построим статическую характеристику объекта регулирования.

Рисунок 5 - Характеристика статическая объекта регулирования

5.2 Статическая характеристика датчика.

Статическая характеристика датчика описывается уравнением:

Y_д= ,

где N=9.

Получим:

Y_д = ,

Для построения характеристики возьмем следующие значения:

Xд	0	1	2	3
Yд	0	1	2	3

По этим значениям построим статическую характеристику датчика. Как видно из рисунка 3 эта характеристика является линейной.

Рисунок 6 - Характеристика статическая датчика

5.3 Статическая характеристика регулятора

Статическая характеристика регулятора описывается уравнением:

Y_р= ,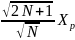

где N=9.

Получим:

Y_р=

Для построения характеристики возьмем следующие значения:

Xр	0	1	2	3
Yр	0	1,45	2,9	4,36

По этим значениям построим статическую характеристику регулятора.

Рисунок 7 - Характеристика статическая регулятора

5.4 Статическая характеристика исполнительного механизма

Статическая характеристика исполнительного механизма описывается уравнением:

Y_и.м = ,

где N=9.

Получим:

Y_и.м= = .

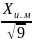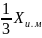Для построения статической характеристики исполнительного механизма возьмем следующие значения:

Xи.м	0	1	2	3
Yи.м	0	0,33	0,67	1

По этим значениям построим статическую характеристику исполнительного механизма

Рисунок 8 - Характеристика статическая исполнительного механизма

Раздел 6 Статические характеристики системы. Рабочая точка. Динамический коэффициент регулирования

6.1 Общая статическая характеристика

Для определения общей статической характеристики цепи обратной связи (ДРИМ) изобразим статические характеристики этих звеньев на общей плоскости.

В первом квадрате находится статическая характеристика датчика, во втором - статическую характеристику регулятора, в третьем – статическую характеристику исполнительного механизма.

Для определения результирующей статической характеристики разобьем ось х_д на равные отрезки. Из точек 1 и 2 проведем перпендикуляры до пересечения с линейной статической характеристикой датчика. Получим точки A₁ и В₁. Из этих точек проведем горизонтали до пересечения с линейной статической характеристикой регулятора. Получим точки А₂ и В₂. Из этих точек опустим перпендикуляры. Горизонтальное положение оси Х_р поменяем на вертикальное. Из новых точек А₂ и В₂ проведем горизонтали до пересечения с соответствующими перпендикулярами в точках A₃ и В₃. Соединим эти точки и получим результирующую статическую характеристику обратной связи.

Рисунок 9 - Характеристика статическая обратной связи