Решение:

1. Рассмотрим сложение М = 6 колебаний с комплексными амплитудами:

тогда комплексная амплитуда результирующего колебания:

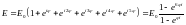
Так как интенсивность – это квадрат амплитуды колебаний:

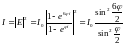
Построим полученную зависимость

Рисунок 2.1

2. При

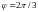
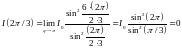
Так как , при наблюдается минимум.

3. Явление дифракции.

Изучите конспект, учебную литературу [1, с.347-425; 2, с.313-387, с.430-444; 3, с.104-144; 4, с.138-215] и ответьте письменно на следующие вопросы:

1. Кратко поясните понятие дифракции, и разницу между теориями дифракции Френеля и Фраунгофера.

Дифракция - это явление, присущее волновым процессам для любого рода волн.

Дифракция Френеля - дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, по условиям, когда основной вклад в интерференционную картину дают границы экрана.

Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды.

2. Приведите формулу дифракции от щели и нарисуйте дифракционную картину. Кратко поясните формулу и рисунок.

Рассмотрим схему наблюдения дифракции Фраунгофера, представленную на рис.3.1. Плоская монохроматическая волна падает нормально на плоскость Щ, где расположена бесконечно длинная щель шириной b (щель можно считать бесконечно длинной, если ее длина намного больше ее ширины. Так при ширине в 0,01 - 0,05 мм длина в несколько миллиметров может считаться бесконечной).

За щелью расположена линза Л, в фокальной плоскости которой находится экран Э. Наличие линзы равносильно тому, что экран расположен как бы на "бесконечном" расстоянии от объекта. Если бы свет распространялся прямолинейно в соответствии с законами геометрической оптики, то в фокальной плоскости линзы получилась бы бесконечно узкая светлая полоса, проходящая через точку N₀ на экране Э. Но в соответствии с принципом Гюйгенса-Френеля каждая точка волнового фронта, достигающего плоскости, где расположена щель, является источником вторичных волн. Тогда лучи, идущие от всех этих вторичных источников под некоторым углом j к первоначальному направлению, образуют плоский волновой фронт и соберутся в фокальной плоскости линзы в т.N_j (рис.3.1).

Рисунок 3.1 – Дифракция Фраунгофера на одной щели

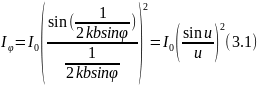
Рисунок 3.2 – Дифракция Фраунгофера на одной щели: распределение интенсивности на экране в зависимости от синуса угла дифракции.

На рис.3.2 приведен график зависимости интенсивности Ij от синуса угла дифракции j. Интенсивность максимальна для направления j_0max=0, совпадающего с направлением распространения падающей волны. Направления, соответствующие последующим максимумам, можно найти из решения задачи поиска экстремума функции.

Рисунок 3.3 – Дифракция Фраунгофера на одной щели: 1 - узкая щель, 2 - широкая щель.

Рассмотрим влияние ширины щели на распределение интенсивности дифракционной картины (рис.3.3). Увеличение ширины щели приводит к приближению первых минимумов к центру дифракционной картины, при этом резкость дифракционного максимума увеличивается (рис.3.3, кривая 2). Соотношение интенсивностей света в отдельных максимумах не изменяется, однако увеличивается абсолютное значение интенсивности, связанное с тем, что с увеличением ширины щели увеличивается энергия проходящего через нее излучения.

В заключении отметим, что дифракция Фраунгофера может наблюдаться и при падении сферической волны на объект, и при отсутствии линзы. Из формулы можно показать, что условия для наблюдения дифракции Фраунгофера имеют вид: b²/𝜆r <<1, b²/𝜆s <<1.

3. Приведите формулу для дифракции Фраунгофера на прямоугольном отверстии и нарисуйте двумерную дифракционную картину. Кратко поясните формулу и рисунок.

Где

a и b – размер сторон прямоугольного отверстия, 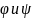– углы дифракции

Рисунок 3.4 – Дифракция Фраунгофера на прямоугольном отверстии

4. Приведите формулу для дифракционной решетки и нарисуйте дифракционную картину. Кратко поясните формулу и рисунок.

Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние щелей.

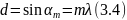
Где, d – период дифракционной решетки; 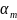– угол к нормали решетки, под которым наблюдается максимум; m=0,±1,±2…; 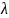– длина волны падающего излучения.

Рисунок 3.5 - Дифракция Фраунгофера на четырех щелях:

а - интерференционный член, б - дифракционный член, в -общий вид дифракционной картины.

Получаем выражение для интенсивности дифрагированных лучей под углом j в виде

Формулу (3.5) можно представить в виде произведения двух членов. Первый член, называемый дифракционным, имеет вид:

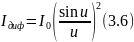
И описывает дифракцию на одной щели размера b. Вид этой функции (рис.3.5 б). Второй член, равный:

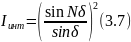
Описывает интерференцию излучения, приходящего от различных щелей, и носит название интерференционного.

5. На примере дифракционной решетки напишите условия возникновения минимума и максимума. Объясните суть условия (критерия) Релея. Напишите выражения для таких параметров, как угловая дисперсия и разрешающая способность дифракционной решетки и кратко поясните их смысл.

На примере дифракционной решетки исходя из рис.3.5, в табл.3.1 приведены условия возникновения минимума и максимума.

главные дифракционные минимумы	sinj =l/b, 2l/b, 3l/b, ....
добавочные интерференционные минимумы	sinj = l/Nd, 2l/Nd, 3l/Nd, ...., (N-1)l/Nd, (N+1)l/Nd,..., (2N-1)l/Nd, (2N+1)l/Nd,...
главные интерференционные максимумы	sinj= 0, l/d, 2l/d, 3l/d, ....

Таблица 3.1 – Условия возникновения минимума и максимума

Условие, введенное Релеем, согласно которому изображения двух близлежащих точек можно видеть реально, если расстояние между центрами дифракционных пятен каждого из изображений меньше радиуса первого темного дифракционного кольца.

Угловая дисперсия дифракционной решетки.

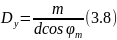
Где 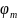– положение m-го максимума.

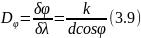
Где 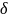– угловое расстояние между двумя спектральными линиями с разностью длин волн 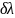; 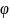– угол дифракции; к=1,2,3…

Разрешающая способность дифрак­ционной решетки. В спектральных приборах с дифракционными решетками положение спектральных линий на плоскости наблюдения дается условием максимумов. Пусть максимум т-го порядка для длины волны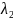  наблюдается под углом  , т.е:

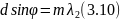
При переходе от максимума к соседнему минимуму разность хода ме­няется на 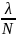 , где N ­число щелей решетки. Следовательно, ми­нимум , наблюдаемый под углом , удовлетворяет условию:

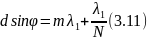
По критерию Рэлея, 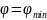, т.е. , или 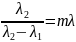  . Так как 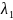  и   близки между собой, т.е. 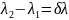, то:

Таким образом, разрешающая способ­ность дифракционной решетки пропорцио­нальна порядку т спектров и числу N ще­лей, т. е. при заданном числе щелей увели­чивается при переходе к спектрам высших порядков. Современные дифракционные решетки обладают довольно высокой раз­решающей способностью (до 2∙10⁵).

6. Что такое дифракция Брэгга, длина волны Брэгга?

Брэгговская дифракция – явление сильного рассеяния волн на периодической решётке рассеивателей при определенных углах падения и длинах волн. Падающая волна последовательно отражается от каждого слоя периодической структуры; все отражённые лучи когерентны и идут в одном направлении, что позволяет им интерферировать. Если все отражённые волны синфазны, то интерференция конструктивна и возникает отражённый луч.

 Дифракции рентгеновских лучей в кристалле: 2dsinθ = mλ, где d расстояние между отражающими кристаллографическими плоскостями, θ угол между падающим лучом и отражающей плоскостью, λ длина волны излучения, m целое положительное число.

Задача 3

На дифракционную решетку, содержащую n штрихов на 1 мм, падает нормально (под прямым углом) монохроматический свет с длиной λ.

Определить:

1. Общее число дифракционных максимумов, которые дает эта решетка.

2. Угол дифракции, соответствующий последнему максимуму.

3. Разрешающую способность дифракционной решетки.

Значения λ и n приведены в табл. 3.1 и табл. 3.2, соответственно.

Таблица 3.1

X	2
λ(мкм)	0,75

Таблица 3.2

Y	4
n	400