Расчет манипуляторов промышленных роботов на жесткость и точность позиционирования

Конструкция роботов представляет пространственные незамкнутые стержневые системы с высокой кинематической подвижностью исполнительных звеньев. Для таких систем главными критериями расчета являются жесткость и динамическая устойчивость конструкции, от которых в значительной степени зависят точность позиционирования, быстрота перемещения детали (производительность) и их масса.

Жесткость манипулятора j представляет собой отношение силы (обычно силы тяжести детали), приложенной к захвату, к перемещению, вызванному силой:

Если направление силы и измеряемой деформации совпадают, то жесткость манипулятора в направлении каждой координатной оси соответственно будет j_x,j_y,j_z. Для промышленных роботов характерна большая податливость звеньев в направлениях, не совпадающих с направлением действующей силы. Жесткость в таких случаях обозначают j_xy,j_zx,j_xz…, где первая буква указывает на направление измерения жесткости, а вторая – на направление действующей силы (например, j_xz – жесткость в направлении оси x от силы, приложенной в направлении оси z).

Суммарная жесткость конструкции робота состоит из собственной и контактной жесткости. Собственная жесткость учитывает деформацию отдельных звеньев: стойки, плеча, захватов и т.д. Контактная жесткость в основном учитывает деформацию в стыках опор подвижных звеньев робота.

При конструировании роботов важно достичь не только требуемой суммарной жесткости, но и необходимо распределить ее между отдельными звеньями с учетом их влияния на величину общего смещения конца руки робота. Это позволяет снизить металлоемкость конструкции и повысить ее динамическую устойчивость.

Конструктивные и расчетные схемы

В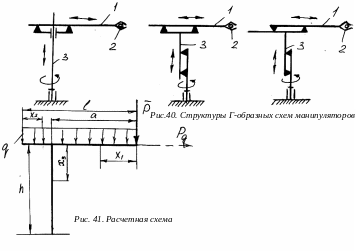 основе большинства конструкций роботов, как отечественного, так и зарубежного производства заложена Г-образная схема.

Кинематика таких роботов обеспечивает перемещение горизонтально расположенного плеча руки 1 с захватом 2 в горизонтальном и вертикальном направлениях и вращения его совместно с вертикальной стойкой 3 вокруг вертикальной оси (рис. 40). Конструкции роботов в основном выполняются с неподвижной или подвижной вертикальной стойкой с постоянным или переменным расстоянием между опорами.

Достаточно общей первоначальной расчетной схемой на жесткость таких конструкций, может быть схема, приведенная на рис. 41, в которой учитывается нагружение робота, как полезной нагрузкой Р, так и собственным весом плеча, представленным распределенной нагрузкой q.

Общее уравнение деформации конструкции в вертикальном f_в и горизонтальном f_г направлениях определяем дифференцированием потенциальной энергии.

Уравнения деформации конструкции

Для определения деформации в горизонтальном направлении вводим добавочную силу P_д, тогда:

,

где Е-модуль упругости

I_l,I_h - моменты инерции соответственно горизонтального и вертикального звеньев,

М₁; М₂; М₃-изгибающие моменты в сечениях x₁, x₂ ,x₃

_{; ; ;}

Подставляя, полученные выражения в исходные формулы, и принимая, Р_д=0, получаем:

Из формул следует, что прогиб горизонтально расположенного плеча в вертикальном направлении вызван деформацией горизонтальной и вертикальной стоек, а смещение плеча в горизонтальном направлении обусловлено только деформацией вертикальной стойки.

Влияние некоторых конструктивных параметров на величину деформации, рассмотрено при максимальном вылете плеча a=l, то есть при максимальной деформации системы. Так при одинаковой длине вертикальной и горизонтальной стоек системы l=h и одинаковой их жесткости I_l=I_h, формулы прогибов принимают вид:

Сравнивая эти деформации, при принятых условиях получим, что деформации в вертикальном направлении более чем в 2,5 раза больше, чем в горизонтальном

Учитывая то, что деформации в вертикальном направлении складываются из деформации вертикальной и горизонтальной стоек, формулу прогиба в данном направлении можно записать:

где - составляющие , учитывающие влияние соответственно горизонтальной и вертикальной стоек на деформацию в вертикальном направлении. При сравнении этих составляющих получим, что прогиб в вертикальном направлении более чем в 3 раза зависит от деформации вертикальной стойки, чем от горизонтальной:

У же из этих сравнений следует, что жесткость вертикальной стойки должна быть значительно выше горизонтальной. Соотношение деформаций системы в вертикальном и горизонтальном направлениях, при различных соотношениях длин l и h и жесткостей и приведено на рис. 42. На этом же рисунке приведены графики, показывающие влияние деформаций вертикального и горизонтального звеньев на прогиб в вертикальном направлении. Эти графики позволяют правильно подобрать соотношение жесткостей этих звеньев для обеспечения минимальных прогибов системы. Приближенно можно рекомендовать для конструкций, в которых длина горизонтального звена меньше длины вертикального, чтобы жесткость вертикального звена была в 4-5 раз больше, чем у горизонтального. При короткой вертикальной стойке по отношению к горизонтальному звену, ее жесткость должна быть выше последнего в 2-3 раза. Зная допустимую величину прогиба в любом направлении, и определив оптимальное соотношение жесткостей вертикального и горизонтального звеньев из графиков (рис. 42) по формулам для и , можно определить размеры их сечений.

Аналогичным путем можно оценить влияние отдельных звеньев на суммарную деформацию конструкции при других направлениях действующих нагрузок.